Try This Combinatorics Problem
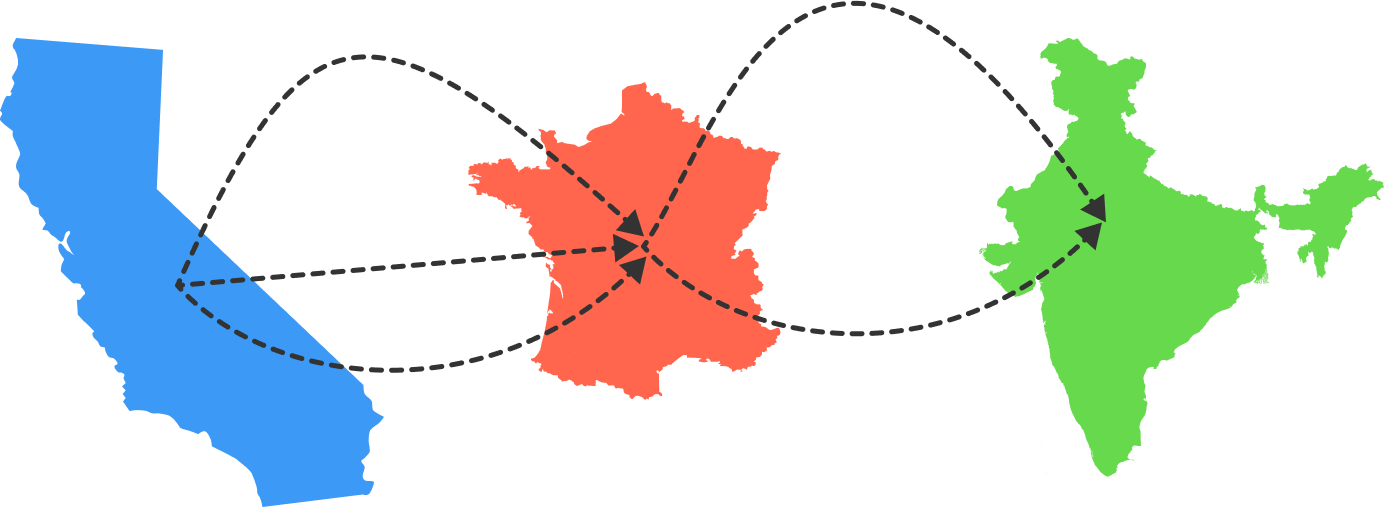
There are 3 flights from California to France, and 2 flights from France to India. Sanjeet wants to fly from California to France and then to India.
How many choices does he have for his flight plan?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
12 solutions
You never said there could only be one trip per leg. The answer is 8.
Exactly the same way.
it is an obvious problem
Log in to reply
I know it is a simple problem, but it is not obvious. Even if it is for you, for some others it may not be that easy.
By the rule of product , there are 3 × 2 = 6 choices he have for his flight plan from California to India.
This one is simple, there are 3 flights from California to France, and 2 flights from France to India. So the rest is simple 3 (the number of flights of California to France)*2 (The number of flights of France to India)=6 (the number of choices available
I agree, but a shorter way to write it (and probably simpler) is: 3 flights from C-F, 2 flights from F-I, so it's C-FxF-I, and that equals 3x2=6, so, there are 6 flights available, get it?
PLUS, it's SUPER easy anyway!!!
By using permutations he can choose in 3P2 ways 3P2=3×2=6 ways
He can use 2 flights for France to India with each flight of California to France hence simply he have 2+2+2=6 choise
It is very simple ; we know that by product rule we can find no. of ways to fly from California to India . therefore he has 3 x 2 = 6 no. of ways to fly from California to India .
Very Simple,......he has - 3*2 i.e. 6 options :) ;)
- Count the France to India routes: FranceIndiaRouteCount=2
- Write FranceToIndiaRouteCount on each California to France route
- Sum up the numbers from step 2
- Realize that step two is basically cloning step 1 results
- Realize that cloning x times a number is multiplication by x
BY basics ot counting of product rule, one procedure diving in separate tasks then separate task multiple, in which first tasks 3 flights and second tasks 2 flight..so, 3*2 is equal to 6 thus correct answer six.
3 x 2 = 6. Which is the answer given which I did get. Though in reality it seems to me that this depends on both of the flights from France to India starting AFTER all of the flights from California have landed in France. If one of the flights from California to France gets to France after 1 of the flights has set off from France to India then the answer is 5 or less (at least as I understand the question). Regards, David
We can use both product rule and sum rule. Product rule:2`3=6 (because after each three flight from California to France these three flights can choose two ways to go to India, so this suits the product rule because these flights from California to France and from France to India can match up) Sum rule: Because we have three different flight to France each flight have their own way to go back to India so it cant be product rule since they are not related to each other anymore. Which means, for Flight 1 we have 3 ways, Flight 2 we have three ways, Flight 3 we also have three ways which sum up to 6. For this type of question we must understand the difference between product and sum rule really before we can understand it, sometimes if u wanna improve your grade you can also think of two side like how can i solve this problem in both sum rule ways and product rule ways.
By the basic counting principle , there are 3 × 2 = 6 ways of going from California to India.
By the rule of product, he has 3 × 2 = 6 ways to fly from California to India.