A probability problem by A Former Brilliant Member
Probability
Level
4
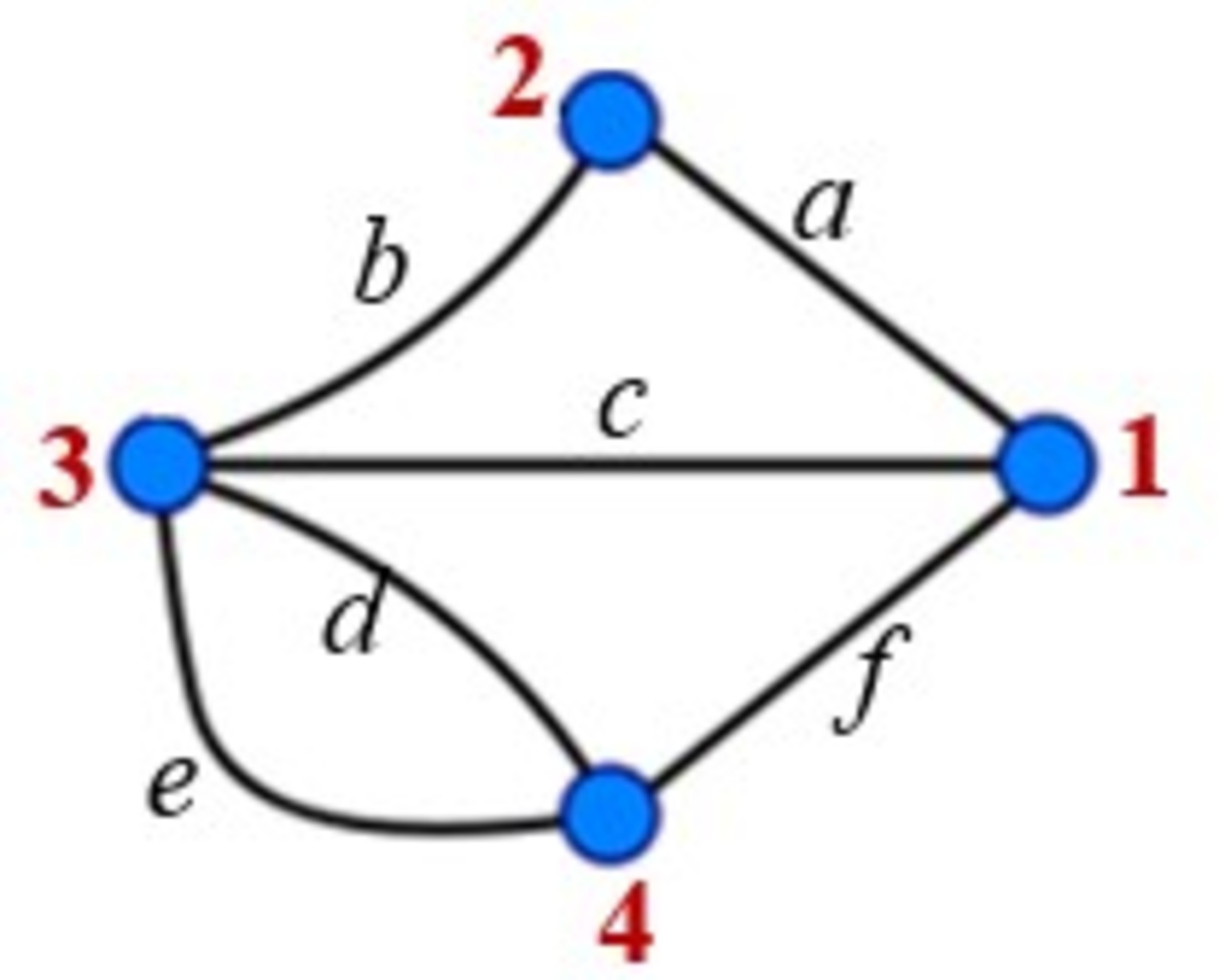In the six-bridge problem as shown by the graph below, how many ways are there of traversing all six bridges (shown as edges here) exactly once? (Please calculate the exact figure).
The answer is 32.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
We now proceed to enumerate all the possibilities. Starting from 1 and returning to 4 contains 16 possibilities: Accoring to differnt branches, we have {a-b-c-f-d-e} {a-b-c-f-e-d} {a-b-d-e-c-f} {a-b-d-f-c-e} {a-b-e-d-c-f} {a-b-e-f-c-d} {c-b-a-f-d-e} {c-b-a-f-e-d} {c-d-e-b-a-f} {c-d-f-a-b-e} {c-e-d-b-a-f} {c-e-f-a-b-d} {f-d-c-a-b-e} {f-d-b-a-c-e} {f-e-b-a-c-d} {f-e-c-a-b-d} Similarly, starting from 4 and returning to 1 also contains 16 possibilities. Hence, we have 32 ways.