Balls in wrong place

Relevant wiki: Principle of Inclusion and Exclusion - Multiple Sets

Let:

$A$ be the condition when ball 1 is in box 1

$B$ be the condition when ball 2 is in box 2

$C$ be the condition when ball 3 is in box 3

By Principle of Inclusion and Exclusion (PIE) we have:

$\begin{aligned} \large |A\cup B \cup C|&= |A| + |B| + |C| - |A \cap B| - |A \cap C| - |B \cap C| + |A \cap B \cap C| \\ \large |A\cup B \cup C|&=7!+7!+7!-6!-6!-6!+5! \\ \large |A\cup B \cup C|&= 3(7!)-3(6!)+5! \end{aligned}$

$\begin{aligned} \large |A\cup B \cup C|'&=8!-\large |A\cup B \cup C| \\ \large |A\cup B \cup C|'&=8!-(3(7!)-3(6!)+5!) \\ \large |A\cup B \cup C|'&=\boxed{27240}\end{aligned}$

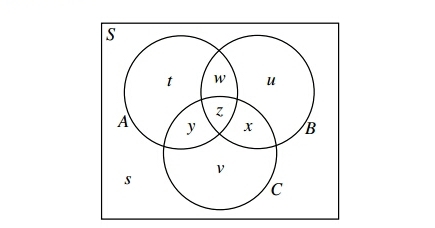
We draw a Venn diagram where $S$ represents all of the ways of placing the 8 balls to 8 boxes with one ball in each box without restriction. Circle $A$ represents all of the ways of placing the 8 balls to 8 boxes with ball 1 going to box 1, Circle $B$ represents all the ways of placing the 8 balls to 8 boxes with ball 2 going to box 2, and Circle $C$ represents all the ways of placing the 8 balls to 8 boxes with ball 3 going to box 3

Here, $s$ represents the number of ways of putting the balls in boxes so that ball 1 is not in box 1 ( $s$ is outside circle $A$ ), ball 2 is not in box 2 ( $s$ is outside circle $B$ ), and ball 3 is not in box 3 ( $s$ is outside circle $C$ ). We want to calculate $s$ .

The total number of ways in $S$ is $8!$ .

Circle $A$ represents the ways when ball 1 is in box 1, and the other 7 balls are placed without restriction. There are $7!$ such ways.

Similarly, the number of ways inside each of circle $B$ and circle $C$ is 7!

In other words, $t + w + y + z = u + w + x + z = v + x + y + z = 7!$

The overlap between circle $A$ and $B$ represents the ways with ball 1 in box 1 and ball 2 in box 2, with the other 6 balls placed without restriction.

There are $6!$ such ways.

Similarly, there are $6!$ ways in the intersection of circles $A$ and $C$ , and circles $B$ and $C$ .

In other words, $w + z = y + z = x + z = 6!$

Finally, the intersection of all three circles represents the ways in which ball 1 is in box 1, ball 2 is in box 2, ball 3 is in box 3, and the other 5 balls are placed without restriction.

There are $5!$ such ways.

In other words, $z = 5!$

Since $z = 5!$

then

$w = x = y = 6! - 5!$

Futhermore

$t = u = v = 7! - 2(6! - 5!) - 5! = 7! - 2(6!) + 5!$

Finally

$s = 8! - (t + u + v + w + x + y + z)$

$s= 8! - 3(7! - 2(6!) + 5!) - 3(6! - 5!) - 5!$

$s= 8! - 3(7!) + 6(6!) - 3(5!) - 3(6!) + 3(5!) - 5!$

$s= 8! - 3(7!) + 3(6!) - 5!$

Therefore,

$s = 40 320 - 3(5040) + 3(720) - 120 = 27 240$

Thus, the number of ways of putting the balls in the boxes with the given restrictions is (27 240