Combinatorics in Geometry

The type of triangle $\Delta ABC$ could be depends on the length of $\overline{BC}$ . That is, the range of values $\overline{BC}$ could become is the open interval $(7,17)$ . The value of $\overline{BC}$ such that $\Delta ABC$ is right is when $\overline{BC} = 13$ . Such is the case when $\overline{BC}$ is the hypotenuse. A length beyond this value would make $\Delta ABC$ an obtuse triangle. However, $\Delta ABC$ will also be a right triangle if $\overline{AB}$ is the hypotenuse. In such case, the length of $\overline{BC} = \sqrt{119}$ . A length less than this value would also make $\Delta ABC$ an obtuse triangle.

Thus, by virtue of linear probability, the probability that $\Delta ABC$ is acute is equal to the probability that $\ \sqrt{119} < \overline {BC} < 13$ . That is,

$P( \overline {BC} < 13) = \large {\frac { 13- \sqrt{119} }{17-7} }$

$= \frac {13- \sqrt{119}}{10}$

This gives us $\large {13 + 119 + 10 =\boxed {142} }$ .

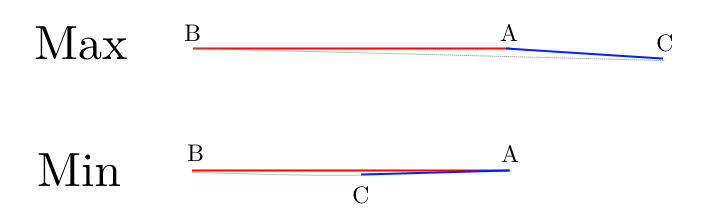
In my diagram above, I am showing that the maximum length of $\overline { BC }$ cannot be more than $\color{#D61F06}{\overline { AB }}$ $+$ $\color{#3D99F6}{\overline { AC }}$ $=17$ . Also, I am showing that the minimum length of $\overline { BC }$ cannot be less than $\color{#D61F06}{\overline { AB }}$ $-$ $\color{#3D99F6}{\overline { AC }}$ $=7$ . So the range of values for $\overline { BC }$ is $17-7=10$ , and we need to find the range of values that makes $\triangle ABC$ acute.

Now, $\triangle ABC$ starts to become acute as $\color{#3D99F6}{\overline { AC }}$ turns clockwise about $A$ and $\angle A<90°$ . Therefore we can work out the maximum possible value of $\overline { BC }$ using Pythagoras:

${ 12 }^{ 2 }+{ 5 }^{ 2 }={ \left( \overline { BC } \right) }^{ 2 }$

$\Rightarrow \overline { BC } =13$

Similarly, we can find the minimum possible value of $\overline { BC }$ when $\angle C<90°$ :

${ 12 }^{ 2 }={ 5 }^{ 2 }+{ \left( \overline { BC } \right) }^{ 2 }$

$\Rightarrow \overline { BC } =\sqrt { 119 }$

So we get a range of $13-\sqrt { 119 }$ for when $\triangle ABC$ is acute. The probability is therefore $\large \frac { 13-\sqrt { 119 } }{ 10 }$ , which cannot be simplified further so we get:

$\Rightarrow a=13$

$\Rightarrow b=119$

$\Rightarrow c=10$

$\large a+b+c=\color{#20A900}{\boxed { 142 }}$

General case:

Say $AB=x, BC=y,$ and WLOG say that $y \leq x.$ The range of possible values for $CA$ is $(x-y, x+y)$ , an interval of length $2y$ . The range of possible values for $CA$ that makes the triangle acute is $(\sqrt{x^2-y^2}, \sqrt{x^2+y^2})$ , so the appropriate probability is $\frac{\sqrt{x^2+y^2}-\sqrt{x^2-y^2}}{2y}$ .