Combinatorics in geometry

Geometry Level 4

We draw $2017$ lines in the plane. These lines cut the plane in parts.

Of these parts exactly $N$ have a finite area.

Of these $N$ parts exactly $K$ are triangles.

Let $x$ be the maximum value of $N$ and let $y$ be the minimum value of $K$ .

Find the value of $x+y$ .

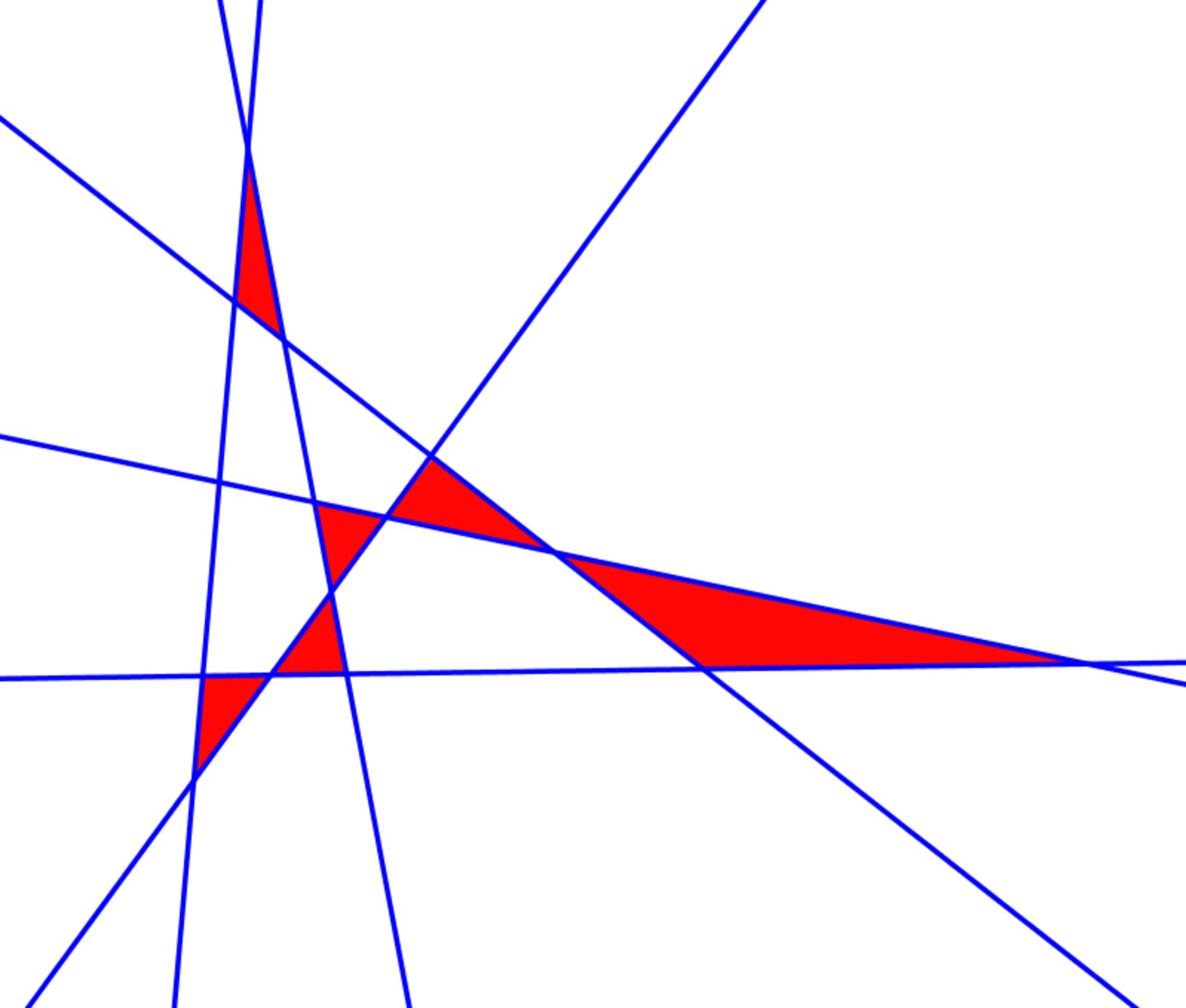
The answer is 2032464.

1 solution

Áron Bán-Szabó
Jun 10, 2017

This is not a really detailed solution, but this can help to solve the problem.

$k$ number of points cut a line into $k+1$ part.

By using induction, we get that $2017$ lines cut the plain into maximum $\frac{1}{2}(2017^2+2017+2)$ parts. From these parts there will be $2(2017)$ parts which have an infinite area.

Let's call the intersections of the straight lines to the vertices. Find the nearest vertices (or one of them) on each straight line. The straight lines which include this vertex define a triangle. There can be no point on either the inside or the perimeter. It is easy to see that there can be maximum two straight lines which have only one side which have vertices. So at least $2015$ straight lines will have a one-one triangle in each side. We calculated each triangle three times.

So $x=\frac{1}{2}(2017^2+2017+2)-4034$ and $y=\frac{1}{3}(4034-2)$ .

The answer is $x+y=\boxed{2032464}$ .

If you look at the report, I agree that $y = 2015$ .

The issue is that in your solution, you thought of y as the minimum number of triangles when N = x. However, this wasn't made explicit in the problem.

Calvin Lin Staff - 3 years, 10 months ago

Combinatorics in geometry

The answer is 2032464.

1 solution

0 pending reports