No Slippage

Probability Level 3

When we place $1 \times 2$ dominoes on a board that isn't completely covered, sometimes we are able to move a domino horizontally or vertically. For example, in this $3 \times 2$ board, the yellow domino can move horizontally while the blue domino is stuck.

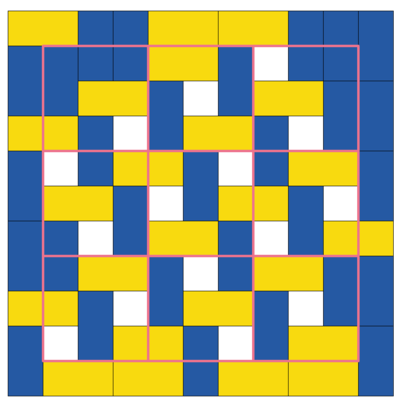
Consider an $8 \times 8$ board tiled with several $1 \times 2$ dominos. What is the minimum number of dominos for which there exists an arrangement in which no domino can move (horizontally or vertically) into another position?

Details and Assumptions:

The dominos are not allowed to stick out of the board or overlap.
We get to choose the placement of the dominos.

The answer is 28.

1 solution

Mark Hennings
Mar 6, 2017

Split the chessboard into the outer ring of squares on the edge, the inner ring of squares "one square in" from the edge, and the centre of $16$ squares.

If we have a rigid placement of dominos, it is impossible for there to be an empty square on the outer ring. If there were could be, there would be an empty square $O$ on the outer ring adjacent to a filled square on the outer ring. This filled square would have to be filled "vertically" (see the diagram), since otherwise that domino could slide onto $O$ . The square $X$ would have to be filled, to stop this vertical domino sliding onto $O$ . If the square $X$ were filled "vertically", the domino filling that square could slide onto $O$ . Thus the square $X$ must be filled horizontally. To stop that domino sliding onto $O$ , the square to the right of $O$ must be filled, and this can only happen "horizontally", yielding a different domino that can slide onto $O$ . A similar argument stops there being an empty square in the corner.

There can be empty squares in the inner ring. If there is such a square, the square between it and the edge must be filled "horizontally" by a domino $A$ . To stop $A$ sliding onto the empty square, it has to be blocked by $B$ , which has to be vertical (so that it cannot itself slide onto the empty square). $B$ is now stopped from sliding onto the empty square by $C$ , which must be horizontal, and $C$ is stopped from sliding onto the empty square by $D$ , which in turn is stopped by sliding onto the empty square by $A$ . Empty squares on the inner ring must be the centre of a $3\times3$ square formed by dominos. If there are two empty squares in the inner ring, thes associated $3\times3$ squares must be disjoint. Fitting $3\times3$ squares around the edge of the chessboard, we readily find that there can only be at most $4$ empty squares in the inner ring.

It is easy to play with what little space is left to see that the largest number of empty square possible is $8$ , making a minimum number of $\boxed{28}$ dominos. The pattern is one of overlapping $3\times3$ squares, with four extra dominos (the centre ones on each edge) added for stability (since the pattern would otherwise need to extend beyond the chessboard).

Moderator note:

The general problem is slightly trickier to argue, because it's not obvious that the above pattern with slight changes must yield an optimal layout.

For the specific $8 \times 8$ case, we show that it's an optimal because

There is no empty square on the outer ring.
Every empty square must be surrounded by 4 dominos in a clockwise / anticlockwise manner.
(some work required) Every $3 \times 3$ square can have at most 2 empty squares.
Hence, we can have at most 8 empty spaces, which means we have at least 28 dominoes

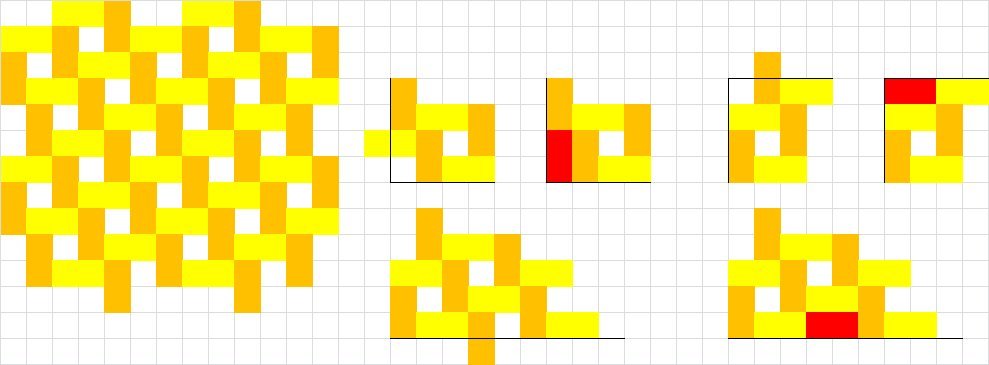
For the $11 \times 11$ case, currently the best that I can do is 53 dominos as shown.
The above argument gives that there are at most 18 empty spaces, but we can only have an odd number of empty spaces. So it shows we have to place at least $\frac{ 121 - 17 } { 2} = 52$ dominoes.
Any ideas on how we could tighten this up?

Note: In the comments, Mark shows that we can achieve 52 dominos!

Indeed, if we apply the herring-bone pattern to a finite board, we only have to patch up the would-be holes at the edges. Every hole on the edge is adjacent to a domino, one half of which is sticking outside the finite board. All we have to do is rotate that domino and we have filled the illegal hole and adjusted the illegally-placed domino. Holes away from the outer ring are unaffected by this.

The game is simply to maximize the number of holes that are not on the edge!

Mark Hennings - 4 years, 3 months ago

Good observations made about

No empty square on the outer ring.
How we must tile around an empty square.

How can we generalize this argument to a larger board? The next one of interest would be $11 \times 11$ . We will need a cleverer argument in place of "It is easy to play with what little space is left to see that the largest number of empty square possible".

Calvin Lin Staff - 4 years, 3 months ago

Well, wherever possible, each domino should be used to bound two empty squares (it cannot bound three or more without being movable). The herring-bone pattern I am using has every domino (apart from the ones at the edge of the board) bounding two empty squares, which is a less experimental argument for $28$ being optimal for the $8\times8$ case, and should give a handle on the more general case.

Indeed, the herring-bone pattern is, to within trivial symmetries, the only pattern of dominos and empty squares that tessellates the plane for which every domino bounds two empty squares. For any particular finite grid, I guess we will try a finite number of options, determining where (in relation to the square) to start the pattern, and in each case see what is needed to shore up the edges of the grid by adding extra dominos.

Mark Hennings - 4 years, 3 months ago

I added details about why I found the $11 \times 11$ case interesting. It's not clear to me how to "locally optimize the truncated pattern and shore up the edges". In particular, the upper left corner seems very inefficient, but I cannot squeeze in 2 empty squares to remove a domino.

Calvin Lin Staff - 4 years, 3 months ago

Except your graphic only has $15$ holes, and so uses $53$ dominos.

Here is one with $17$ holes and $52$ dominos. The red dominos are the variations from the herringbone pattern

Mark Hennings - 4 years, 3 months ago

Oh thanks! I guess I didn't use the pattern efficiently since the lower right corner also isn't nicely packed.

Calvin Lin Staff - 4 years, 3 months ago

My full pattern works for $5n+1$ , not $3n+2$ . I could come up with other pictures, though...

Mark Hennings - 4 years, 3 months ago

(I do not have the result for $3n + 2 \times 3n+2$ squares. I've edited my note.)

Here's what I have done:

Show that with any $n \times m$ board (bigger than $2 \times 2$ ), we can use this covering and fill in the other ring:
Using the pattern where we place an orange domino on over (1,1) and (1,2), and place a yellow domino over (2,1) and (3,1). [Using your grid squares in the entire image, my (1,1) corresponds to your (2, 4)].
Then, block out the $n \times m$ board and look at the outer ring. If there are any holes on the boundary, if we proceed in an anitclockwise manner (say from (1,1) ), we will always hit a sticking out domino just before an empty spce. As such, we can push this domino in to fill in the space.
Claim that "if every internal domino is used in 2 interlocking $3 \times 3$ squares, then that's the best we can do".
Assuming this claim, then it is satisfied for the pattern, and hence this is the best that we can do.

However, I'm not perfectly happy with the argument in 2. I do feel that it's a handwavy argument about optimization, and would prefer to see it properly dealt with. I tried to rigorize it by using the fact that "in every $3 \times 3$ square, there are at most 2 empty squares" to bound the number of empty squares (and hence the number of dominoes). However, this doesn't work, because it is too aggressive. In the herring-bone pattern, there are some of our cut-up squares which would only contain 1 empty square (In the $11 \times 11$ example, this would be the very central square ).

Calvin Lin Staff - 4 years, 3 months ago

No Slippage

The answer is 28.

1 solution

Moderator note:

0 pending reports