Combinatorics Senior Challenges-III
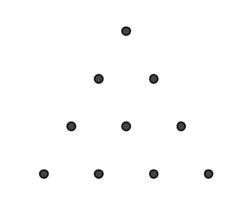Given a 10 point equilateral triangular lattice of points distance one
apart, how many distinct equilateral triangles can be formed with the vertices of the lattice?
This problem is not original. The image does not show a 10 point equilateral triangular lattice, so is not the required lattice. This problem is part of this set .
The answer is 15.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Nice reasoning, Parth; those tilted triangles are easy to miss.
There is in fact a general formula for this type of problem; if the lattice is made up of 2 n ( n + 1 ) points, (in this case n = 4 ), then the number of triangles is
T n = 2 4 ( n − 1 ) ( n ) ( n + 1 ) ( n + 2 ) ,
as per this link , (where I have adjusted the formula to account for the offset given in the link).
i didn't understand this part: "Side length 31/2: there are two triangles for this case, both tilted."
what's triangle is this? can you explain?
Log in to reply
I believe that Parth meant a side length of 3 . Such a triangle is formed using the following vertices:
-
the second point in from the left on the lowest level,
-
the third point in from the left on the next level up, and
-
the first point in from the left on the third level up.
A second equilateral triangle congruent to this one is formed in the same way going from the right rather than the left.
I think the question asks for a lattice made up of 55 points!!
Combinatorics: The Fine Art of Counting .best book isnt it?
We will partition the problem based on the side lengths of the triangles. Assume the lattice is oriented with 4 points horizontal at the base
• Side length 1: there are 3+2+1 triangles pointing up and 2+1 triangles pointing down or a total of 9 for this case.
• Side length 2: there are 2+1 triangles pointing up for a total of 3 in this case.
• Side length 3: just one triangle for this case.
• Side length 31/2: there are two triangles for this case, both tilted.
• Thus the total would appear to be 9+3+1+2 = 15