Combinatronics JEE

Probability Level 5

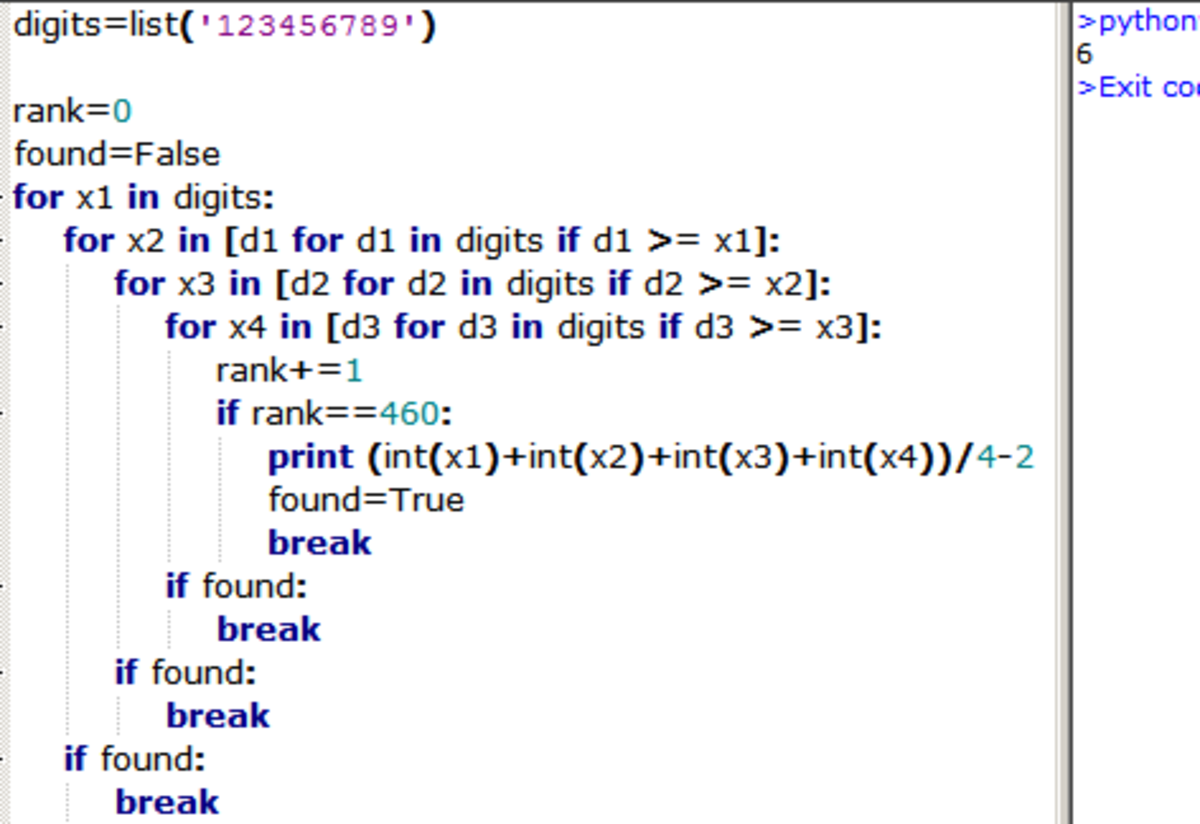
All four digit numbers of the form $\overline{x_1 x_2 x_3 x_4}$ form by using the digits 1 to 9 such that $x_1 \leq x_2 \leq x_3 \leq x_4$ and are list in ascending order (smallest to biggest).

If the number with rank 460 is of the form $\overline{abcd}$ , find $\frac {a+b+c+d}{4} - 2$ .

The answer is 6.00.

2 solutions

Kunal Verma
May 3, 2015

For numbers between $1000$ and $2000$ , we observe there are:- $(9 \ + \ 8 \ + \ 7 \ + \ 6 \ + \ 5 \ + \ 4 \ + \ 3 \ + \ 2 \ + \ 1) \ + \ (8 \ + \ 7 \ + \ ... \ 1) \ + \ ... \ 1 \ = \ 165$ such numbers. Now between $2000$ and $3000$ , due to the reduction of $10 \ - \ 20$ range, There will be $(8 \ + \ 7 \ + \ ... \ 1) \ + \ (7 \ + \ 6 \ ... \ 1) \ ... \ 1 \ = \ 120$ such numbers. This will go on. In this way summing up the number of solutions for $1000$ to $6000$ , we get:- $165 \ + \ 120 \ + \ 84 \ + \ 56 \ + \ 35 \ = \ 460$ This tells us our required number is the last number such representable in the range of $5000$ to $6000$ which is obviously $5999$ . Thus $\frac { 5+9+9+9 }{ 4 } -\quad 2\quad =\quad \boxed { 6 }$

Bill Bell
May 24, 2015

This is not something one can do during an examination, of course.

Combinatronics JEE

The answer is 6.00.

2 solutions

0 pending reports