Combining functions
Given a function
defined as
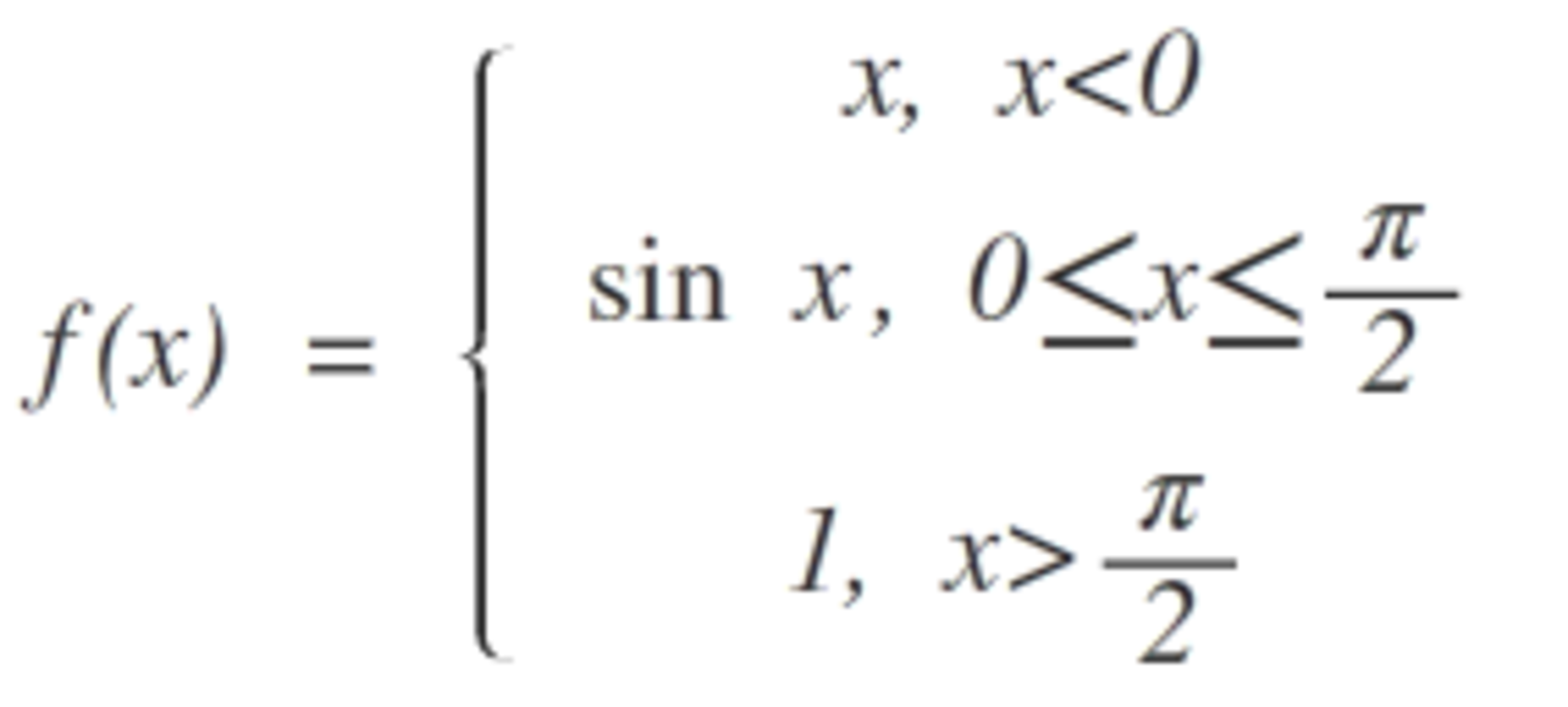 Then
Then
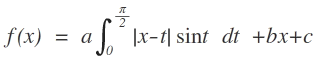 Find the value of
.
Find the value of
.
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let g ( x ) = ∫ 0 π / 2 ∣ x − t ∣ s i n ( t ) d t .
Setting s = x − t , we get the integral
∫ x − π / 2 x ∣ s ∣ s i n ( x − s ) d s
which can be evaluated by naturally considering the cases x < 0 , 0 ≤ x ≤ π / 2 , and x > π / 2 to simplify the ∣ s ∣ function. This yields the piecewise function
⎩ ⎪ ⎨ ⎪ ⎧ − ∫ x − π / 2 x s ⋅ s i n ( x − s ) d s ∫ 0 x s ⋅ s i n ( x − s ) d s − ∫ x − π / 2 0 s ⋅ s i n ( x − s ) d s ∫ x − π / 2 x s ⋅ s i n ( x − s ) d s x < 0 0 ≤ x ≤ π / 2 x > π / 2
which simplifies to
\left\{ \begin{array}{11} 1-x & x < 0 \\ x+1-2sin(x) & 0\leq x\leq \pi/2 \\ x-1 & x > \pi/2 \end{array} \right. .
Now since we know f ( x ) = a ⋅ g ( x ) + b x + c , we end up needing to solve the equations a + b = 0 , c − a = 1 , a + c = 0 , b − a = 1 , and − 2 a = 1 , which has the solution a = − 1 / 2 , b = 1 / 2 , and c = 1 / 2 , yielding an answer of 8 .