Come Closer!

Electricity and Magnetism Level 4

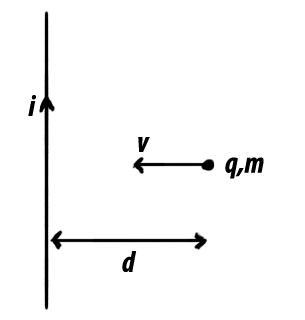A Charged Particle of Mass $m$ and Charge $q$ is thrown with an initial velocity of $v$ towards an infinite wire carrying a current $i$ from an initial distance of $d$ .

If the minimum separation (in meters) between the particle and the wire, during the course of time, is $\ell$ , then Evaluate $\ell\times 10^{49}$ to the nearest Integer

Details and Assumptions:

$\mu_o = 4\pi \times 10^{-7}\frac{\text{N}}{\text{A}^2}$
$i = 5\text{ A}$
$m = 0.08\text{ g}$
$d = 4\text{ m}$
$v = 1.386\frac{\text{m}}{\text{s}}$
$q = 1\text{ C}$

The answer is 28.

1 solution

Ronak Agarwal
Jul 20, 2014

Come closer

Since magnetic force is doing no work on the particle hence particle's velocity is constant. At any instant of time it is revolving in a circle of radius $R$ given by $R=\frac { mv }{ qB }$ .

Now let it revolves an angle $d\theta$ hence $\overset { \rightarrow }{ dR } ={ -dRcos\theta }\overset { \wedge }{ i } -dRsin\theta \overset { \wedge }{ j }$ where $\theta$ is the angle made by the velocity of the particle with the horizontal.

Now $dx=-Rcos\theta d\theta$

$B=\frac { { \mu }_{ 0 }i }{ 2\pi x } \Rightarrow R=\frac { 2\pi xmv }{ { \mu }_{ 0 }qi }$

So we have got $\int _{ d }^{ { x }_{ min } }{ \frac { dx }{ x } } =\int _{ 0 }^{ \frac { \pi }{ 2 } }{ \frac { 2\pi mv }{ { \mu }_{ 0 }qi } (-cos\theta d\theta ) }$

Solving ${ x }_{ min }=d{ e }^{ \frac { -2\pi mv }{ { \mu }_{ o }qi } }$

Put the values we have $\boxed { { x }_{ min }=28\times { 10 }^{ -49 } }$

this is standard prob..!! But your approach is really nice it is different from my..!! Nice work

Deepanshu Gupta - 6 years, 9 months ago

It seems there is something wrong with my approach. Could you please correct me where I am going wrong?

(I drew the same diagram as in your solution) NOW, $\overrightarrow { F } =q(\overrightarrow { v } \times \overrightarrow { B } )\quad \quad ..\quad (Lorentz\quad Force\quad on\quad particle)\\ F=q[({ v }_{ x }\hat { i } +\quad { v }_{ y }\hat { j } )\times B(-\hat { k } )]\\ F=q[{ v }_{ x }B(\hat { j } )-{ v }_{ y }B(\hat { i } )]\\ \overrightarrow { a } =\frac { q }{ m } (-{ v }_{ y }B\hat { i } +{ v }_{ x }B\hat { j } )\quad \quad \quad ..\quad \quad (Acceleration\quad of\quad particle)\\ v\frac { dv }{ dx } =\frac { q }{ m } (-{ v }_{ y }B\hat { i } )\quad \quad \quad \quad \quad \quad ..\quad \quad (Considering\quad only\quad along\quad x-axis)\\ \\ (v\quad above\quad is\quad the\quad initial\quad velocity\quad with\quad which\quad it's\quad thrown)\\ \\ v\frac { dv }{ dx } =\frac { -qB }{ m } \sqrt { { v }^{ 2 }-{ { v }_{ x } }^{ 2 } } \\ v\int { \frac { dv }{ \sqrt { { v }^{ 2 }-{ { v }_{ x } }^{ 2 } } } } =\frac { -qB }{ m } \int { dx } \\ On\quad integrating\quad above,\\ v\log { |v+\sqrt { { v }^{ 2 }-{ { v }_{ x } }^{ 2 } } | } =\frac { -qBx }{ m } \\ Now,\quad I\quad put\quad { v }_{ x }=0,\quad to\quad find\quad minimum\quad deistance\quad of\quad seperation\quad horizontally\\ from\quad the\quad wire.\quad Hence,\quad x\quad on\quad the\quad right\quad hand\quad side\quad of\quad the\quad above\quad equation\\ gives\quad me\quad the\quad minimum\quad distance\quad of\quad seperation.\\ \\ SO,\\ vlog|2v|=\frac { -qBx }{ m } \\ which\quad gives,\\ x=\frac { =mvlog|2v| }{ qB } \\ \\ However,\quad from\quad what\quad I\quad understand,\quad B=\frac { { \mu }_{ \o }I }{ 2\Pi x } \\ However,\quad using\quad the\quad above\quad expression\quad in\quad the\quad equation\quad above,\quad x\quad cut\quad out\quad on\quad both\quad sides.\\ What\quad am\quad I\quad doing\quad wrong?$

Vedabit Saha - 6 years, 10 months ago

The main mistake you made is that when you write

$v\frac { dv }{ dx } =\frac { q }{ m } (-{ B }_{ y }\hat { i } )$ is incorrect.

Instead you should write ${ v }_{ x }\frac { d{ v }_{ x } }{ dx } =\frac { q }{ m } (-{ B }_{ y }\hat { i } )$

So your integration would have become

$\int { \frac { { v }_{ x }d{ v }_{ x } }{ \sqrt { { v }^{ 2 }-{ v }_{ x }^{ 2 } } } } =\frac { -qBx }{ m }$

Ronak Agarwal - 6 years, 10 months ago

Ah! Of course! Sorry for the trouble -.-' I forgot to see the component of acceleration along with velocity. Gotta be more careful xD Thanks a lot :)

Vedabit Saha - 6 years, 10 months ago

Woah i thought it would be too clumsy using force analsys, ,you did pretty well, man,, awesome,, way,,, :D

Mvs Saketh - 6 years, 10 months ago

i solve other method

Anil malviya - 6 years, 10 months ago

Can you please tell your method

Ronak Agarwal - 6 years, 10 months ago

if electric field is introduced perpendicular then.....

saket khandal - 5 years, 11 months ago

done in same way

Ayush Garg - 6 years, 10 months ago

Yes, got a solution which is more easier than any other of these posted here....and just a tiny bit more easier than Ronak's. I would be posting it when I completely learn using the Daum editor and also when the internet speeds become normal again(after about 7 days)...Keep posting and loving physics.....

Tushar Gopalka - 6 years, 10 months ago

Overall I understand the solution but in this part I'm still geting confuse to understand it :/

"Now let it revolves an angle $d\theta$ hence $\overset { \rightarrow }{ dR } ={ -dRcos\theta }\overset { \wedge }{ i } -dRsin\theta \overset { \wedge }{ j }$ where $\theta$ is the angle made by the velocity of the particle with the horizontal.

Now $dx=-Rcos\theta d\theta$ "

Could you draw the diagram of the vector,please?

Resha Dwika Hefni Al-Fahsi - 5 years, 1 month ago

Come Closer!

The answer is 28.

1 solution

0 pending reports