Cometary orbit
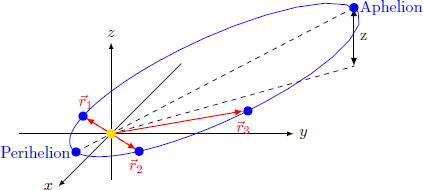
While observing near-Earth celestial bodies, astronomers discover a small, faint comet. Shortly after its discovery, this celestial body escapes direct observation and is only found again twice many months later. These two observed positions of the comet in the three-dimensional coordinate system are r 1 = ⎝ ⎛ − 1 − 1 0 ⎠ ⎞ , r 2 = ⎝ ⎛ 1 1 0 ⎠ ⎞ , r 3 = ⎝ ⎛ 0 3 0 . 5 ⎠ ⎞ in astronomical units.
Reconstructing the complete orbit of the comet, what is the distance z from the ecliptic of the comet at the most remote point (aphelion), to 2 decimal places?
Details and Assumptions:
The comet orbit is an ellipse, with the sun at the origin
(
r
=
0
)
corresponding to one of the two foci of the ellipse. The
x
y
-plane represents the ecliptic (orbital plane of the earth).
The answer is 1.28.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
 The ellipse of the comet lies in a plane that passes through the origin
and the three given vectors
The ellipse of the comet lies in a plane that passes through the origin
and the three given vectors
The normal to the plane can be found by cross multiplying r 1 with r 3 .
n = r 1 × r 3
After normalizing n , we can find two mutually perpendicular unit vectors u 1 , u 2 that are orthogonal to n , and thus span the plane.
Now define the reference frame using the three vectors
R = [ u 1 , u 2 , n ]
Then if p 0 and p 1 are the coordinate vectors in the absolute frame and in the frame we just defined, we have the following relation
p 0 = R p 1
Note that the choice of u 1 and u 2 is not unique.
Now we can find the coordinate vectors of r 1 , r 2 and r 3 with respect to the new frame,
[ r 1 ′ , r 2 ′ , r 3 ′ ] = R T [ r 1 , r 2 , r 3 ]
Note that each of the three vectors is of the form
r i ′ = ⎣ ⎡ x i ′ y i ′ 0 ⎦ ⎤
Now we use the polar equation of an ellipse with one of its foci at the origin
It is given by
r = 1 − e cos ( θ − ϕ ) a ( 1 − e 2 )
where ϕ is the angle that the major axis makes with the x'-axis.
To fully specify the ellipse, we need to find the parameters a (the major semi-axis) , e (the eccentricity), and ϕ (the tilt angle). To that end, by reciprocating the above equation we get
r 1 = a ′ + b ′ cos θ + c ′ sin θ
where
a ′ = a ( 1 − e 2 ) 1
b ′ = − a ( 1 − e 2 ) e cos ϕ
c ′ = − a ( 1 − e 2 ) e sin ϕ
Given the three sets of coordinates of the known vectors in the plane, we can write a linear system of three equations
in the three unknowns a ′ , b ′ and c ′ . Solving the linear system, we can determine that
ϕ = tan − 1 ( b ′ c ′ ) + π
Next e can be determined as
e = − a ′ cos ϕ b ′
and
a = a ′ ( 1 − e 2 ) 1
In the final step, we determine the position vector of the aphelion as that corresponding to θ = ϕ , hence
r ∗ = 1 − e a ( 1 − e 2 ) = a ( 1 + e )
From which, the aphelion has coordinates
x ′ = a ( 1 + e ) cos ( ϕ )
y ′ = a ( 1 + e ) sin ( ϕ )
z ′ = 0
Using these coordinates we find the coordinates of aphelion with respect to the absolute frame as
r = R r ′
where R is defined above. And the answer will be the z-coordinate obtained from the last equation.
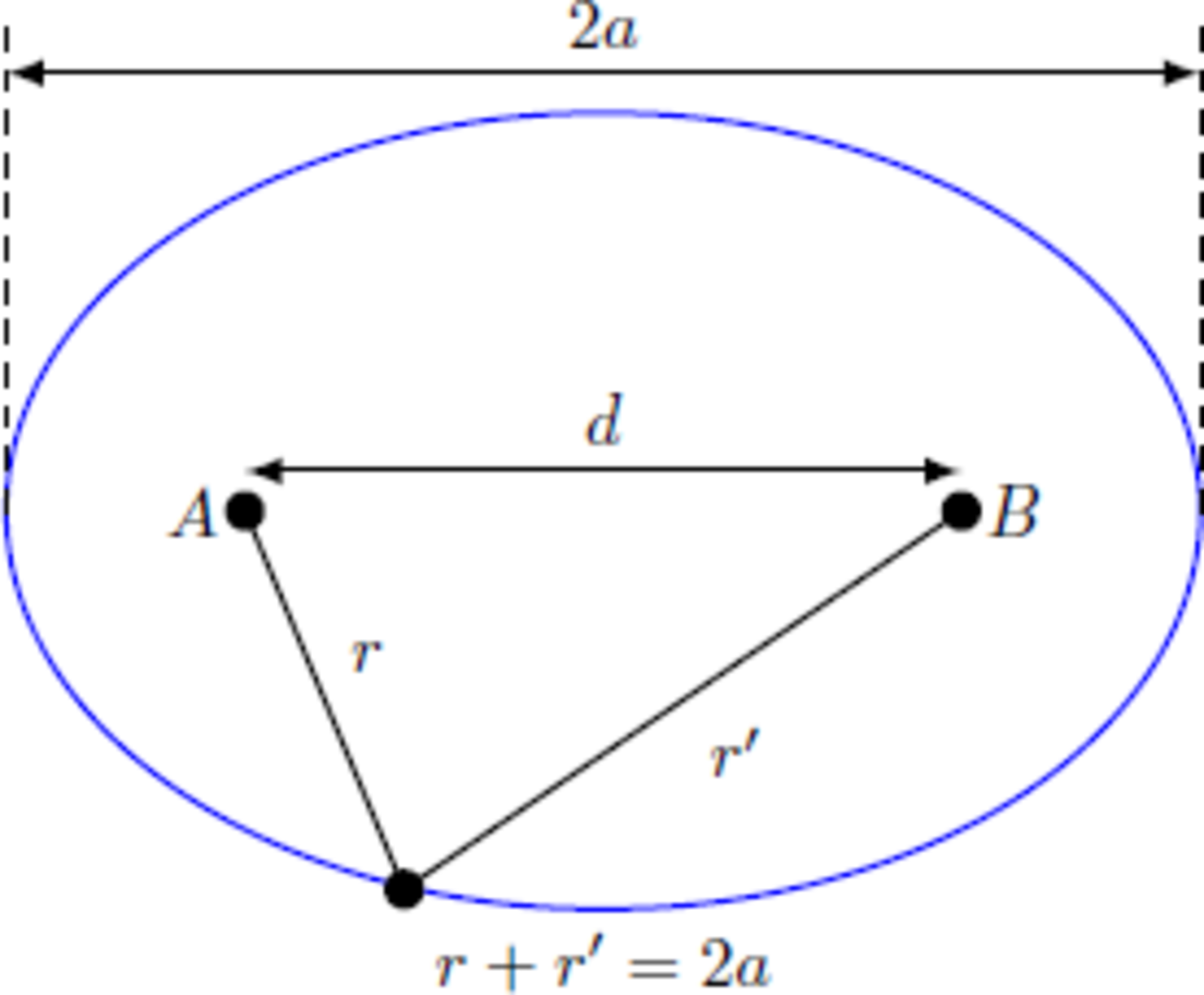
Since r 1 = − r 2 , both vectors are perpendicular to the large half-axis of the ellipse The comet has different radial distances { r 1 = r 2 = 1 2 + 1 2 + 0 2 = 2 ≈ 1 . 4 1 4 r 3 = 0 2 + 3 2 + ( 2 1 ) 2 = 3 7 / 2 ≈ 3 . 0 4 1 from the sun. The angle ϕ = ∠ ( r 2 , r 3 ) between the vectors is calculated with the dot product r 2 ⋅ r 3 ⇒ ϕ = r 2 r 3 cos ϕ = 1 ⋅ 0 + 1 ⋅ 3 + 0 ⋅ 2 1 = 3 = arccos r 2 r 3 r 2 ⋅ r 3 ≈ 4 5 . 7 7 ∘ The distances r 2 ′ , r 3 ′ to the other focus read { r 2 ′ = r 2 2 + d 2 r 3 ′ = r 3 2 + d 2 − 2 r 3 d sin ϕ with the distance d between the two foci. The sum r + r ′ = 2 a is a constant ( a : large half-axis). Therefore, we get a system of equations for the unknown a and d : ⇒ ⇒ { 2 a = r 2 + r 2 2 + d 2 2 a = r 3 + r 3 2 + d 2 − 2 r 3 d sin ϕ { ( 2 a − r 2 ) 2 = r 2 2 + d 2 ( 2 a − r 3 ) 2 = r 3 2 + d 2 − 2 r 3 d sin ϕ { 4 a 2 − 4 a r 2 = d 2 4 a 2 − 4 a r 3 = d 2 − 2 r 3 d sin ϕ If one subtracts both equations from each other, then one gets 4 a ( r 3 − r 2 ) ⇒ d = 2 r 3 d sin ϕ = 2 a r 3 sin ϕ r 3 − r 2 Insertion into the first line of the equation system results 4 a 2 − 4 a r 2 ⇒ a ⇒ d = 4 a 2 ( r 3 sin ϕ r 3 − r 2 ) 2 = 1 − ( r 3 sin ϕ r 3 − r 2 ) 2 r 2 ≈ 3 . 1 9 5 = 2 a r 3 sin ϕ r 3 − r 2 ≈ 4 . 7 7 1 The maximum distance of the comet from the sun is thus r max = a + 2 d ≈ 5 . 5 8 1
Now the tilt angle θ of the ellipse in relation to the ecliptic has to be determined. A vector orthogonal to the plane results from the cross product ⇒ ⇒ r 2 × r 3 ( r 2 × r 3 ) ⋅ e z θ z max = ⎝ ⎛ 1 ⋅ 2 1 − 0 ⋅ 3 0 ⋅ 0 − 1 ⋅ 2 1 1 ⋅ 3 − 1 ⋅ 0 ⎠ ⎞ = ⎝ ⎛ 2 1 − 2 1 3 ⎠ ⎞ = ∣ r 2 × r 3 ∣ cos θ = arccos ∣ r 2 × r 3 ∣ ( r 2 × r 3 ) ⋅ e z ≈ 1 3 . 2 6 ∘ = r max sin θ ≈ 1 . 2 8