Coming back home after a few strikes
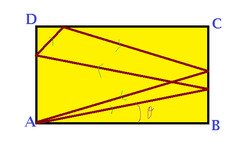 From one corner A of a fixed regular billiards table ABCD placed on a horizontal surface. A ball of mass m=2kg and negligible dimensions is projected in the horizontal plane. The coefficient of restitution is 0.5 for every collision. It strikes the sides in order BC , AD , DC ,BC , and then returns to the same point A then the angle of initial projection it makes with side AB is
θ
From one corner A of a fixed regular billiards table ABCD placed on a horizontal surface. A ball of mass m=2kg and negligible dimensions is projected in the horizontal plane. The coefficient of restitution is 0.5 for every collision. It strikes the sides in order BC , AD , DC ,BC , and then returns to the same point A then the angle of initial projection it makes with side AB is
θ
If the ratio of sides AB:BC is 5:1, find ⌊ 1 0 0 t a n θ ⌋ .
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Nice work Milun,
Although I think that you have an extra = sign in the penultimate line also K isn't the midpoint of A P 2 .
The last lines should read c o s θ a ( 1 + e 1 + e 2 1 + e 3 1 ) = s i n θ b ( 1 + e 1 )
We are given e = 0 . 5 and a / b = 5 in the question. Substituting in these values gives 5 t a n θ × ( 1 + 2 + 4 + 8 ) = ( 1 + 2 ) 2 5 t a n θ = 1 Or 1 0 0 t a n θ = 4
Log in to reply
Well k is the midpoint of AP2 I've just not shown it in the diagram. BTW thanks for pointing out the typos
What a lengthy question! Well, It felt awesome, when answer matched!
t 2 = e u c o s θ a = u s i n θ K P 2 .... P 1 → P 2 .....K is the mid point of A P 2
t 3 = e 2 u c o s θ D P 3 = u s i n θ P 2 D ..... P 2 → P 3
t 4 = e 2 u c o s θ P 3 C = e u s i n θ C P 4 ..... P 3 → P 4
t 5 = e 3 u c o s θ a = e u s i n θ P 4 B .... P 4 → A
u c o s θ a + e u c o s θ a + e 2 u c o s θ D P 3 + e 2 u c o s θ P 3 C + e 3 u c o s θ a = u s i n θ B P 1 + u s i n θ K P 2 + u s i n θ P 2 D + e u s i n θ C P 4 + e u s i n θ P 4 B
c o s θ a ( 1 + e 1 + e 2 1 + e 3 1 ) = s i n θ b ( 1 + e 1 )
e = b c o s θ − a s i n θ a s i n θ