Coming Out The Same Way

Classical Mechanics Level 4

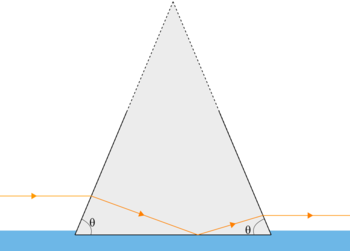
A glass prism whose cross-section is an isosceles triangle stands with its (horizontal) base in water; the angles that its two equal sides make with the base are each $\theta$ .

An incident ray of light, above and parallel to the water surface and perpendicular to the prism's axis, enters the prism and is internally reflected at the glass-water interface and re-emerges into the air. Taking the refractive indices of glass and water to be $\frac{3}{2}$ and $\frac{4}{3}$ , respectively.

Calculate the minimum value of $\theta$ (in radians) for total internal reflection to be possible.

Give your answer to 3 decimal places.

The answer is 0.45163.

1 solution

Harsh Poonia
Feb 16, 2019

Hope you get the idea

Observe that the angle of incidence of the incident ray is $\frac {\pi}{2}-\theta$ radians as the ray is parallel to the base.
Now using Snell's Law for the refraction, $\dfrac {\sin(\pi/2-\theta)}{\sin r_1} = \mu \implies \dfrac {\cos(\theta)}{\sin r_1} = \dfrac {3}{2}$ . $\cdot\cdot\cdot\cdot\cdot\cdot Eqn(1)$
Next, for Total Internal Reflection to take place, $\sin(r_1+\theta) > \dfrac {\mu_2}{\mu_1} \implies \sin(r_1+\theta)> \dfrac { \frac{4}{3}}{ \frac{3}{2}} = \dfrac{8}{9} .$
$\implies r_1+\theta > \arcsin(8/9) \approx 62.734$ degrees $\cdot\cdot\cdot\cdot\cdot\cdot Eqn(2)$

Finally using $(1)$ and $(2)$ , solve for the minimum value of $\boxed {\theta \approx 0.451}$ radians that satisfies this.

Coming Out The Same Way

The answer is 0.45163.

1 solution

0 pending reports