Common area of two ellipses
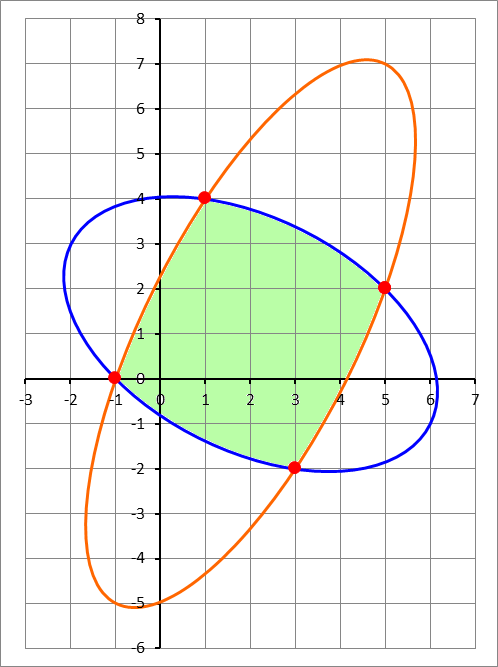
Two ellipses have the equations
7 x 2 + 8 x y + 1 3 y 2 − 3 6 x − 4 2 y − 4 3 = 0
(drawn in blue), and
3 3 x 2 − 2 8 x y + 1 2 y 2 − 1 0 4 x + 3 2 y − 1 3 7 = 0
(drawn in orange). Find the area of the region that is common to both ellipses (shaded in light green). If this area is A , then enter ⌊ 1 0 0 0 A ⌋ as your answer.
The answer is 22905.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
I will take advantage of the graph provided to get a much simpler solution.
Rotate the ellipses with respect to their center ( 2 , 1 ) so that the coordinates of the intersection points are ( ± 5 , ± 5 ) . In these rotated axes centered at ( 2 , 1 ) the ellipses have equations of the form a 2 x 2 + b 2 y 2 = 1 where the major semi-axis a of each one is read from the graph and b can be calculated substituting one of the intersection points. After little manipulation, the ellipses become:
- Blue ellipse: x 2 + 3 y 2 = 2 0 , with major semi-axis a = 2 5
- Orange ellipse: y 2 + 8 x 2 = 4 5 , with major semi-axis a = 3 5
The square has an area of 2 0 . We just need to calculate the extra area limited by the sides of the square and the four arches.
We get integrals of the form ∫ − x 0 x 0 a 2 − x 2 d x which are quite straightforward to solve using the variable change x = a sin θ , d x = a cos θ d θ :
∫ − x 0 x 0 a 2 − x 2 d x = 2 × ∫ 0 arcsin ( a x 0 ) cos 2 θ d θ = 2 × ∫ 0 arcsin ( a x 0 ) cos 2 θ d θ = 2 × ∫ 0 arcsin ( a x 0 ) 2 1 + 2 1 cos 2 θ d θ = [ θ + 2 1 sin 2 θ ] 0 arcsin ( a x 0 )
Using x 0 = 5 and the values of a for each ellipse we obtain:
- A b l u e [ θ + 2 1 sin 2 θ ] 0 arcsin ( 2 5 5 ) ≈ 1 . 0 4 5 9 9 8
- A o r a n g e [ θ + 2 1 sin 2 θ ] 0 arcsin ( 3 5 5 ) ≈ 0 . 4 0 6 7 7 2
The total area is A = A s q u a r e + 2 × A b l u e + 2 × A o r a n g e ≈ 2 2 . 9 0 5 5 4 0 ⟹ ⌊ 1 0 0 0 A ⌋ = 2 2 9 0 5
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 |
|
The given equation of the first ellipse can be written using matrices as
r T A r + b T r + c = 0 ( 1 )
where
r = [ x y ] T
A = [ 7 4 4 1 3 ]
b T = [ − 3 6 − 4 2 ]
c = − 4 3
The first step is to find the center of this ellipse. It is given by
r 0 = − 2 1 A − 1 b ( 2 )
One can verify that equation (1) be re-written as,
( r − r 0 ) T A ( r − r 0 ) = − c + r 0 T A r 0 ( 3 )
Define the matrix Q as follows
Q = − c + r 0 T A r 0 A ( 4 )
then, from equation (3) and (4), we obtain
( r − r 0 ) T Q ( r − r 0 ) = 1 ( 5 )
The next step is to diagonalize Q , and write it as Q = R D R T
The procedure is as follows,
Let θ = 2 1 tan − 1 Q 1 1 − Q 2 2 2 Q 1 2 ( 6 )
Then
R = [ cos θ sin θ − sin θ cos θ ] ( 7 )
and
D = diag { d 1 1 , d 2 2 } ( 8 . 1 )
with
d 1 1 = Q 1 1 cos 2 θ + Q 2 2 sin 2 θ + 2 Q 1 2 cos θ sin θ ( 8 . 2 )
d 2 2 = Q 1 1 sin 2 θ + Q 2 2 cos 2 θ − 2 Q 1 2 cos θ sin θ ( 8 . 3 )
Replacing matrix Q in equation (5) by its diagonalized form, we obtain
( r − r 0 ) T R D R T ( r − r 0 ) = 1 ( 9 )
For an ellipse, the diagonal matrix D has positive entries, and therefore can be factored as D = D 2 1 D 2 1
Using this factorization, and defining the vector
u = D 2 1 R T ( r − r 0 ) ( 1 0 )
then it follows that u T u = 1 , thus vector u is a unit vector, and can therefore be parameterized as u = [ cos t , sin t ] T .
Solving for r in terms of u gives,
r = r 0 + R D − 2 1 u = r 0 + V u ( 1 1 )
The columns of matrix V are vectors extending along the major and minor axes directions and having lengths of the semi-major
and semi-minor axes.
The same procedure can be applied to the second ellipse, and we'll end up with the following parametric equations for
the two ellipses,
r 1 ( t ) = r C 1 + V 1 u 1 ( t ) ( 1 2 . 1 )
r 2 ( s ) = r C 2 + V 2 u 2 ( s ) ( 1 2 . 2 )
Performing the calculations detailed above, the reader can verify that,
r C 1 = r C 2 = [ 2 1 ] T
V 1 = ⎣ ⎢ ⎡ 4 − 2 3 2 3 4 ⎦ ⎥ ⎤
V 2 = ⎣ ⎢ ⎡ 2 3 − 2 2 3 3 6 ⎦ ⎥ ⎤
We next have to find the points of intersection of the two ellipses, so we set up the equation,
r 1 ( t ) = r 2 ( s ) ⟹ r C 1 + V 1 u 1 ( t ) = r C 2 + V 2 u 2 ( s ) ( 1 3 )
Solving for u 1 ( t ) , we obtain,
u 1 ( t ) = V 1 − 1 ( r C 2 − r C 1 + V 2 u 2 ( s ) ) = e + F u 2 ( s ) ( 1 4 )
where e = V 1 − 1 ( r C 2 − r C 1 ) and F = V 1 − 1 V 2
Since u 1 is a unit vector, we have u 1 T u 1 = 1 , and this leads to,
( e + F u 2 ) T ( e + F u 2 ) = 1 ( 1 5 )
Expanding the left hand side of (15),
u 2 T F T F u 2 + 2 u 2 T F T e + e T e = 1 ( 1 6 )
For reference, let's define G = F T F , h = 2 F T e , q = e T e − 1 , then equation (16) can be written as,
u 2 T G u 2 + u 2 T h + q = 0 ( 1 7 )
Recall that u 2 = [ cos s , sin s ] T , thus expanding equation (17) yields,
G 1 1 cos 2 s + G 2 2 sin 2 s + 2 G 1 2 sin s cos s + h 1 cos s + h 2 sin s + q = 0 ( 1 8 )
Using the identities cos 2 s = 2 1 ( 1 + cos ( 2 s ) ) , and sin 2 s = 2 1 ( 1 − cos ( 2 s ) ) as well as 2 sin s cos s = sin ( 2 s ) , equation (18) becomes,
c 1 cos s + c 2 sin s + c 3 cos 2 s + c 4 sin 2 s + c 5 = 0 ( 1 9 )
where c 1 = h 1 , c 2 = h 2 , c 3 = 2 1 ( G 1 1 − G 2 2 ) , c 4 = G 1 2 , c 5 = q + 2 1 ( G 1 1 + G 2 2 )
After performing all the calculations above, equation (19) produces four solutions, and they are,
s 1 = 0 . 3 3 9 8 3 6 9 0 9 s 2 = 2 . 8 0 1 7 5 5 7 4 4 s 3 = 3 . 4 8 1 4 2 9 5 6 3 s 4 = 5 . 9 4 3 3 4 8 3 9 8
The corresponding values for parameter t of the first ellipse are,
t 1 = 1 . 0 4 7 1 9 7 5 5 1 t 2 = 2 . 0 9 4 3 9 5 1 0 2 t 3 = 4 . 1 8 8 7 9 0 2 0 5 t 4 = 5 . 2 3 5 9 8 7 7 5 6
The four solution for s (and also the four corresponding solutions of t ) correspond in turn to the Cartesian points:
P 1 = ( 5 , 2 ) , P 2 = ( 1 , 4 ) , P 3 = ( − 1 , 0 ) , P 4 = ( 3 , − 2 )
The region common to both ellipses is bounded by the first ellipse for t ∈ [ t 1 , t 2 ] and for t ∈ [ t 3 , t 4 ] and is bounded by the second ellipse for s ∈ [ s 2 , s 3 ] and for s ∈ [ s 4 , s 1 + 2 π ]
The area enclosed by the parametric curve r ( t ) = ( x ( t ) , y ( t ) ) whose t -derivative is r ′ ( t ) = ( x ′ ( t ) , y ′ ( t ) ) is given by the formula
Area = 2 1 ∣ ∣ ∣ ∣ ∫ t i t f x ( t ) y ′ ( t ) − x ′ ( t ) y ( t ) d t ∣ ∣ ∣ ∣ ( 2 0 )
If we extend the vector r ( t ) and its t -derivative into three dimensions, by padding our r ( t ) and r ′ ( t ) with a zero z coordinate, then the above integral can be written conveniently using cross product notation as,
Area = 2 1 ∣ ∣ ∣ ∣ ∫ t i t f ( r ( t ) × r ′ ( t ) ) z d t ∣ ∣ ∣ ∣ ( 2 1 )
where ( ⋅ ) z is the z coordinate of its vector argument. We have to use this formula four times corresponding to the four intervals that we have. Now let's see what this evaluation entails. We have
r ( t ) = r C + V u
If V = [ v 1 v 2 ] , where v 1 and v 2 are the columns of V , then we have,
r ( t ) = r C + v 1 cos t + v 2 sin t
and its t -derivative is,
r ′ ( t ) = − v 1 sin t + v 2 cos t
Hence,
r ( t ) × r ′ ( t ) = − ( r C × v 1 ) sin t + ( r C × v 2 ) cos t + ( v 1 × v 2 ) ( cos 2 t + sin 2 t )
which simplifies to,
r ( t ) × r ′ ( t ) = − ( r C × v 1 ) sin t + ( r C × v 2 ) cos t + v 1 × v 2
Evaluating the area integral over a given interval [ t i , t f ] yields,
A k = 2 1 ( ( r C × v 1 ) z ( cos t f − cos t i ) + ( r C × v 2 ) z ( sin t f − sin t i ) + ( v 1 × v 2 ) z ( t f − t i ) ) k = 1 , 2 , 3 , 4
In this particular problem, and since r C 1 = r C 2 we can shift the center of our parametric curves to the origin, and this simplifies the above formula into
A k = 2 1 ( v 1 × v 2 ) z ( t f − t i ) k = 1 , 2 , 3 , 4
From matrix V 1 and V 2 above, we have, for the first ellipse, ( v 1 × v 2 ) z = 3 2 0 , and for the second ellipse, ( v 1 × v 2 ) z = 2 2 4 5
Plugging in the t and s values we found, the area is given by,
Area = 2 1 ( 3 2 0 ( t 2 − t 1 + t 4 − t 3 ) + 2 2 4 5 ( s 3 − s 2 + s 1 + 2 π − s 4 ) )
This evaluates to, Area = A = 2 2 . 9 0 5 5 4 0 0 0 4 3 , and this makes the answer ⌊ 1 0 0 0 A ⌋ = 2 2 9 0 5 .
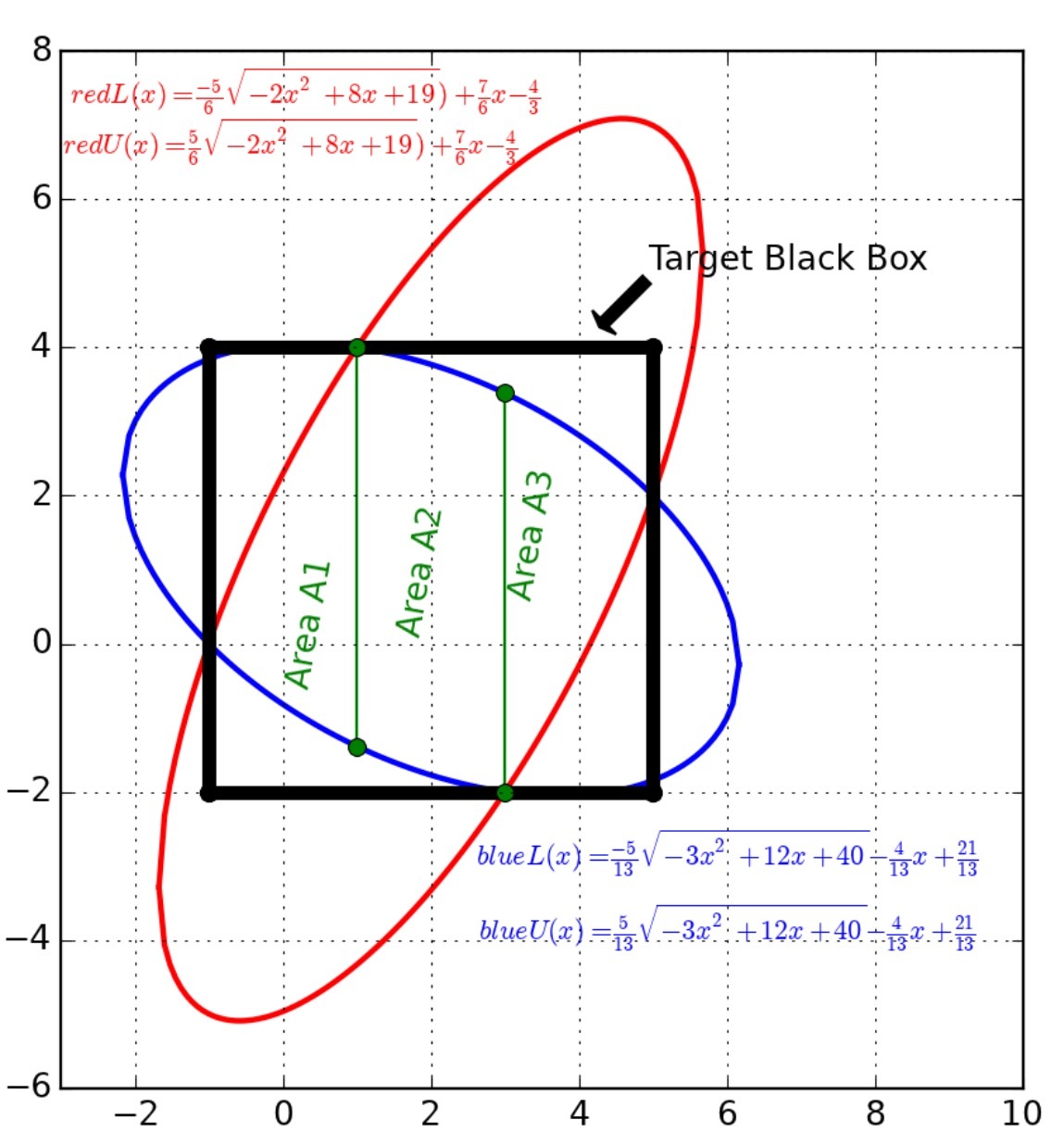
Solving the two ellipse equations, the points of intersection are P ( 1 , 4 ) , Q ( 5 , 2 ) , R ( 3 , − 2 ) , and S ( − 1 , 0 ) .
Using the distance formula, the sides of quadrilateral P Q R S are P Q = Q R = R S = P R = 2 0 and the diagonals are P R = Q S = 4 0 , therefore P Q R S is a square with an area of A P Q R S = 2 0 .
The equation of the line with P Q is y = − 2 1 x + 2 9 and the equation of the line with P R is y = 2 x + 2 .
The equation of the upper part of the blue ellipse rearranges to y = 1 3 1 ( 5 − 3 x 2 + 1 2 x + 4 0 − 4 x + 2 1 ) , and the equation of the upper part of the orange ellipse rearranges to y = 6 1 ( 5 − 2 x 2 + 8 x + 1 9 + 7 x − 8 ) .
The area of the section between the blue ellipse and P Q is then A P Q = ∫ 1 5 ( ( 1 3 1 ( 5 − 3 x 2 + 1 2 x + 4 0 − 4 x + 2 1 ) ) − ( − 2 1 x + 2 9 ) ) d x , and the area of the section between the orange ellipse and P R is A P R = ∫ − 1 1 ( ( 6 1 ( 5 − 2 x 2 + 8 x + 1 9 + 7 x − 8 ) ) − ( 2 x + 2 ) ) d x .
By symmetry, A R S = A P Q and A Q R = A P R , so the total shaded area is A = 2 A P Q + 2 A P R + A P Q R S ≈ 2 2 . 9 0 5 5 , which makes ⌊ 1 0 0 0 A ⌋ = 2 2 9 0 5 .