Common part volume of six crossing cylinders

Outline:

• show how the volume of our solid is related to its surface area
• set up a set of axis vectors
• identify the area of one cylindric region
• calculate it and hence the total area
• calculate the volume

Relation between volume and surface area . Note that the boundary of our solid is restricted by cylinders, each of which has the same radius $R=1$ and all of which have their axes pass through the solid's centre. Consider a cylinder and take a ring-shaped part of its surface area $A=2πrh$ . Also consider the volume that is enclosed between the surface area and the centre of the solid, by connecting each point of the area boundary by a straight line to the centre. The enclosed volume is $V=\int_0^R 2πr\cdot h\frac{r}{R}dr=\frac{2}{3}πR^2h=\frac{1}{3}RA$ . Using standard arguments, this can easily be generalised to any section of cylindrical area. Because we have $R=1$ , for our purposes we can use $V=\frac{1}{3}A$

Axis vectors . I will place a dodecahedron such that is centre is at the origin, its 'top' face is parallel to the $xy$ -plane, having a vertex on the first quadrant of the $xz$ -plane, i.e. $y=0, x>0 , z>0$ .

Now unit normal vectors to the six uppermost planes are $n_0=(0,0,1) \text{ and } \vec{n}_i=(\frac{2}{\sqrt{5}}\cosα_i, \frac{2}{\sqrt{5}}\sinα_i, \frac{1}{\sqrt{5}}) \text { for i=1, 2, 3, 4, 5}$ Here $α_1=π/5, α_2=3π/5, α_3=π, α_4=7π/5, α_5=9π/5$ . Check that $|\vec{n}_i|=1$ and $\vec{n}_0 \cdot \vec{n}_1 = \vec{n}_1 \cdot \vec{n}_2$ etc.

Identify a cylindrical area Note that the vertical cylinder $x^2+y^2=1$ defines the surface of the solid at the point $\vec{p}=(1,0,0)$ , because its axis $(0,0,1)$ is at right angles to $\vec{p}$ . We are looking for the (boundaries of) the area that is defined by this cylinder.

For any point $\vec{p}$ on the vertical cylinder we can set $\vec{p}=(\cos θ, \sin θ, z)$ . If also $|\vec{n}_i×\vec{p}|=1$ , it is on the cylinder around axis $n_i$ as well. $|\vec{n}_i×\vec{p}|^2=\frac{1}{5}(2 \sin α \cdot z-\sin θ, \cos θ - 2\cos α \cdot z, 2 \cos α \sin θ - 2 \sin α \cos θ)^2 =\frac{1}{5}(4z^2-4\cos(θ-α)+1+4\sin^2(θ-α)=1$ which solves to $z=\frac{\cos(θ-α)\pm \sqrt{5}\cos (θ-α)}{2}$ so that every value of $θ$ generates two points on the intersection of the two cylinders: $\vec{p}_1=(\cos θ,\sin θ,φ \cos(θ-α)), p_2=(\cosθ,\sin θ,-\frac{1}{φ} \cos(θ-α))$ where $φ=\frac{1+\sqrt{5}}{2}$ .

Note that $\vec{p}_1$ and $\vec{p}_2$ coincide when $θ-α=\pm \frac{π}{2}$ (mod π), so these values for θ reflect an intersection that is on the solid's surface.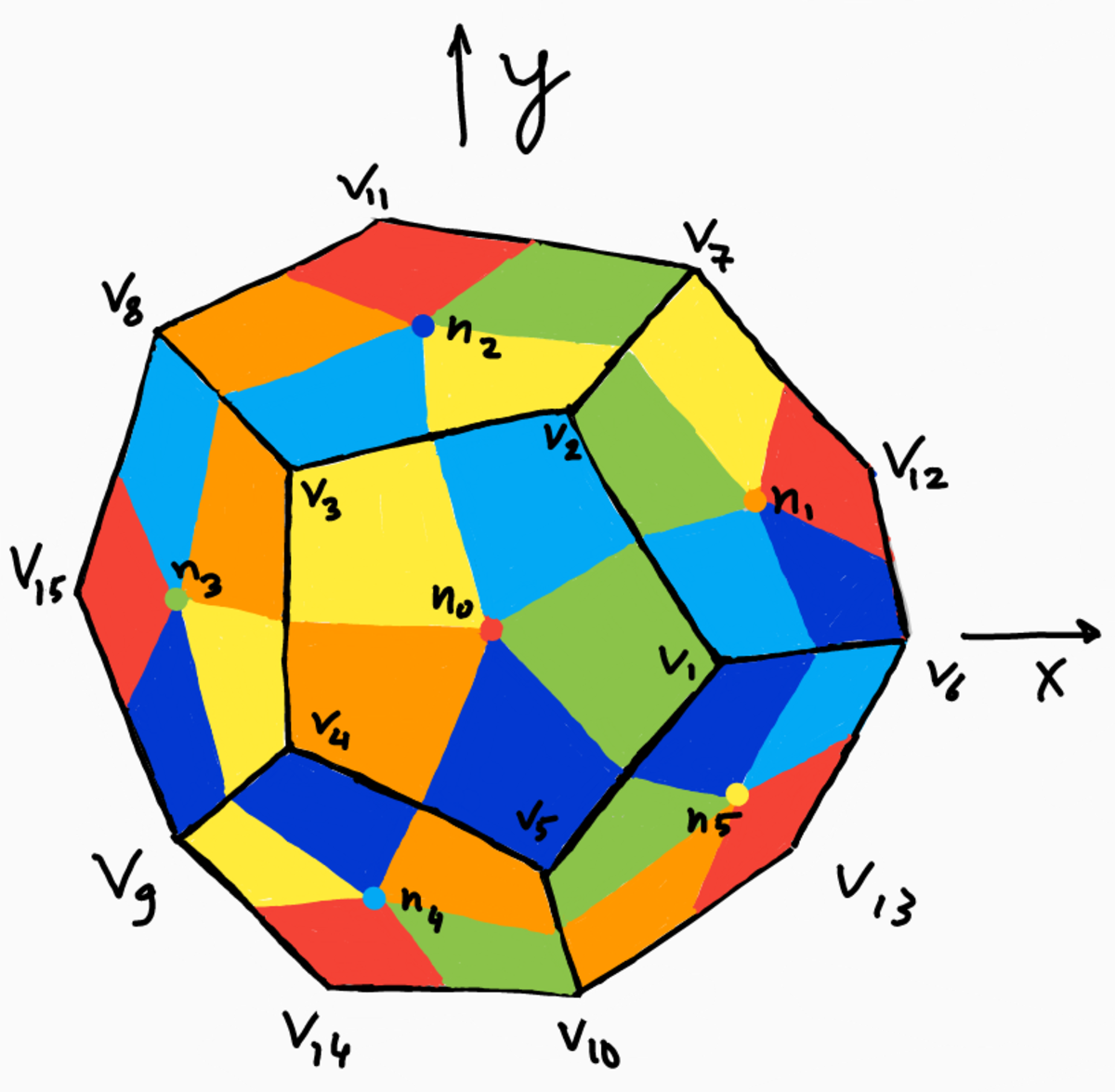 Fig. 1a. Top view, as seen from the positive z-axis

Fig. 1b. Side view, as seen from near the positive x-axis (18° towards the y-axis)

Fig. 1 Free-hand sketches of a dodecahedron that is circumscribed about the unit sphere. Colours show which cylinder will locally define the resulting solid. Axes of the cylinders are marked by dots or arrows in corresponding colours.

It turns out that the area containing point $(1,0,0)$ is bordered by the intersection of cylinder 0 with cylinder 2 for positive y and by the intersection of cylinder 0 with cylinder 4 for negative y. [Cylinders numbered according to their axis vector indices.]

Calculate area and volume For cylinder 2, the upper boundary (where $\vec{p}_1$ and $\vec{p}_2$ coincide) is $α+\frac{π}{2}$ (mod π) = $\frac{π}{10}$ . The following integral gives half the area: $A_{half section} = \int_0^{π/10} (φ+φ^{-1}) |\cos(θ-α_2)|dθ=\sqrt{5}\int_{-3π/5}^{-π/2}|\cos u| du=\sqrt{5}(1-\sin(3π/5))=\sqrt{5}(1-\sqrt{\frac{5+\sqrt{5}}{8}})$

The total area consists of $12×5×2 =120$ times this area, and hence the volume equals one third of that:

$V=40\sqrt{5}(1-\sqrt{\frac{5+\sqrt{5}}{8}})=40\sqrt{5}-10\sqrt{10}\sqrt{5+\sqrt{5}}\approx 4.3776$

Sanity check: the volume should be slightly larger than that of a sphere of radius 1, which is $\frac {4}{3}π1^3\approx 4.19$ .

The answer to submit then is $40+5+10=\boxed{55}$