Common Tangent Mania

Level pending

Let β \beta be a positive integer and ∣ x ∣ > 1 |x| > 1 and f ( x ) = ∑ j = 0 ∞ ( 1 x β + j + 1 − x β + j ) f(x) = \sum_{j = 0}^{\infty} (\dfrac{1}{x^{\beta + j + 1} - x^{\beta + j}}) and g ( x ) = a x 2 + b x + c g(x) = ax^2 + bx + c .

If f ( 3 ) = g ( 3 ) f(3) = g(3) and f ( x ) f(x) and g ( x ) g(x) have a common tangent at x = 2 x = 2 and a + b + c = 1 α α ∗ λ β − w + β + λ α β − w a + b + c = \dfrac{1}{\alpha^{\alpha} * \lambda^{\beta - w}} + \dfrac{\beta + \lambda}{\alpha^{\beta - w}} , where α , λ \alpha, \lambda and w w are coprime positive integers, find α + λ + w \alpha + \lambda + w .

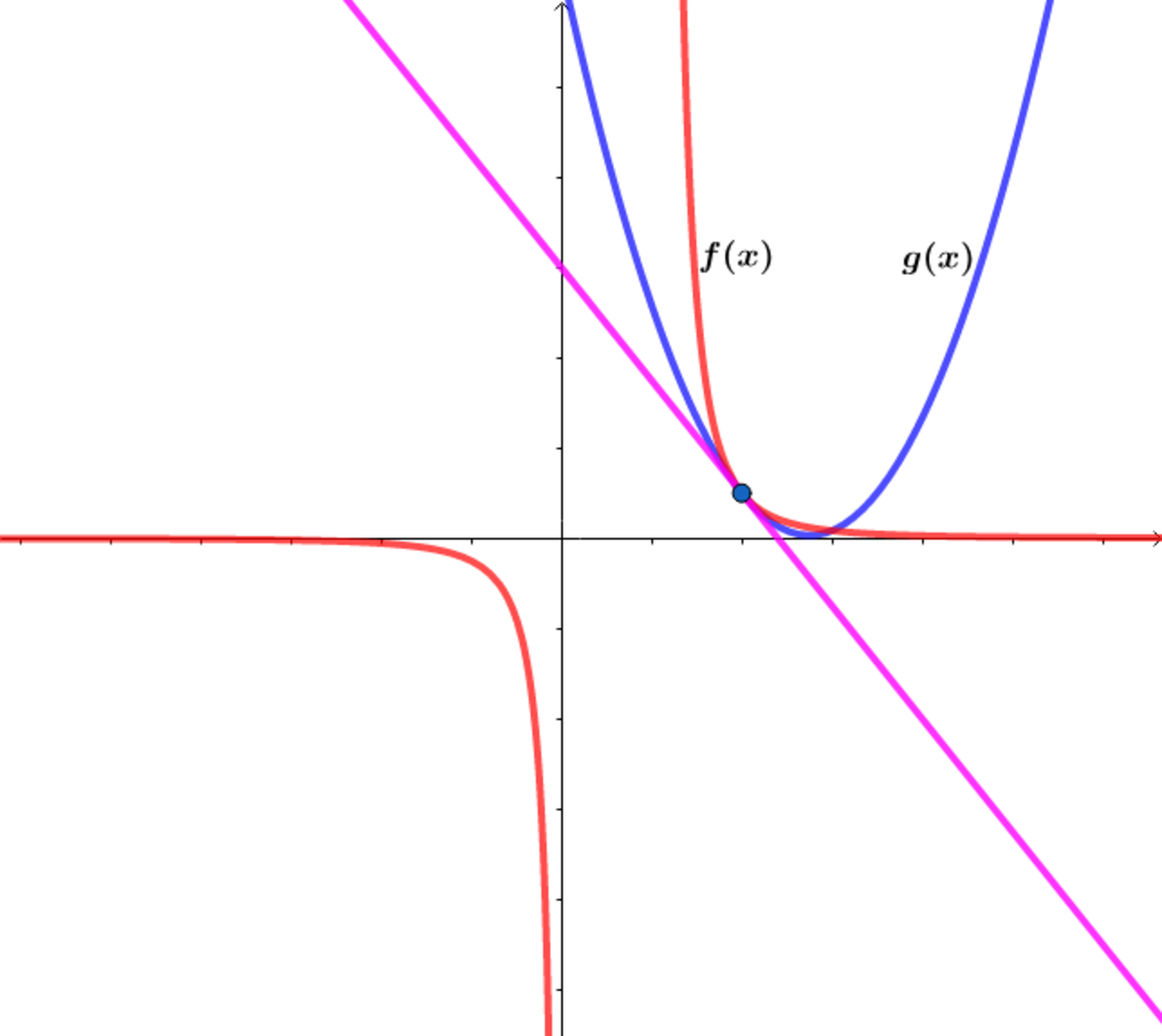
I used β = 2 \beta = 2 for the above graph.


The answer is 6.

Rocco Dalto by Rocco Dalto , 67, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Rocco Dalto
Jul 21, 2018

For β ∈ N \beta \in \mathbb{N} and ∣ x ∣ > 1 |x| > 1 .

f ( x ) = ∑ n = 0 ∞ 1 x β + n + 1 − x β + n = 1 x β ( x − 1 ) ∑ 0 ∞ ( 1 x ) n = 1 x β − 1 ( x − 1 ) 2 f(x) = \sum_{n = 0}^{\infty} \dfrac{1}{x^{\beta + n + 1} - x^{\beta + n}} = \dfrac{1}{x^{\beta}(x - 1)}\sum_{0}^{\infty} (\dfrac{1}{x})^{n} = \dfrac{1}{x^{\beta - 1}(x - 1)^2}

Let g ( x ) = a x 2 + b x + c g(x) = ax^2 + bx + c .

f ( 3 ) = g ( 3 ) ⟹ 9 a + 3 b + c = 1 4 ∗ 3 β − 1 f(3) = g(3) \implies \boxed{9a + 3b + c = \dfrac{1}{4 * 3^{\beta - 1}}}

f ( x ) f(x) and g ( x ) g(x) have a common tangent at x = 2 ⟹ f ( 2 ) = g ( 2 ) x = 2 \implies f(2) = g(2) and d d x ( f ( x ) ) ∣ x = 2 = d d x ( g ( x ) ) ∣ x = 2 \dfrac{d}{dx}(f(x))|_{x = 2} = \dfrac{d}{dx}(g(x))|_{x = 2} .

f ( 2 ) = g ( 2 ) ⟹ 4 a + 2 b + c = 1 2 β − 1 f(2) = g(2) \implies \boxed{4a + 2b + c = \dfrac{1}{2^{\beta - 1}}}

d d x ( f ( x ) ) = β − 1 − ( β + 1 ) x x β ( x − 1 ) 3 \dfrac{d}{dx}(f(x)) = \dfrac{\beta - 1 - (\beta + 1)x}{x^{\beta} (x - 1)^3} and d d x ( g ( x ) ) = 2 a x + b \dfrac{d}{dx}(g(x)) = 2ax + b .

d d x ( f ( x ) ) ∣ x = 2 = d d x ( g ( x ) ) ∣ x = 2 ⟹ 4 a + b = − β + 3 2 β \dfrac{d}{dx}(f(x))|_{x = 2} = \dfrac{d}{dx}(g(x))|_{x = 2} \implies \boxed{4a + b = -\dfrac{\beta + 3}{2^{\beta}}}

Solving the system

4 a + 2 b + c = 1 2 β − 1 4a + 2b + c = \dfrac{1}{2^{\beta - 1}}

9 a + 3 b + c = 1 4 ∗ 3 β − 1 9a + 3b + c = \dfrac{1}{4 * 3^{\beta - 1}}

4 a + b = − β + 3 2 β 4a + b = -\dfrac{\beta + 3}{2^{\beta}}

we obtain:

5 a + b = 1 4 ∗ 3 β − 1 − 1 2 β − 1 5a + b = \dfrac{1}{4 * 3^{\beta - 1}} - \dfrac{1}{2^{\beta - 1}}

4 a + b = − β + 3 2 β 4a + b = -\dfrac{\beta + 3}{2^{\beta}}

⟹ a = 1 4 ∗ 3 β − 1 − 1 2 β − 1 + β + 3 2 β \implies a = \dfrac{1}{4 * 3^{\beta - 1}} - \dfrac{1}{2^{\beta - 1}} + \dfrac{\beta + 3}{2^{\beta}}

b = − 1 3 β − 1 + 4 2 β − 1 − 5 ( β + 3 ) 2 β \:\ \:\ \:\ \:\ \:\ b = -\dfrac{1}{3^{\beta - 1}} + \dfrac{4}{2^{\beta - 1}} - \dfrac{5(\beta + 3)}{2^{\beta}}

c = 1 3 β − 1 − 3 2 β − 1 + 6 ( β + 3 ) 2 β \:\ \:\ \:\ \:\ \:\ c = \dfrac{1}{3^{\beta - 1}} - \dfrac{3}{2^{\beta - 1}} + \dfrac{6(\beta + 3)}{2^{\beta}}

⟹ a + b + c = 1 4 ∗ 3 β − 1 + β + 3 2 β − 1 = \implies a + b + c = \dfrac{1}{4 * 3^{\beta - 1}} + \dfrac{\beta + 3}{2^{\beta - 1}} = 1 2 2 ∗ 3 β − 1 + β + 3 2 β − 1 = \dfrac{1}{2^2 * 3^{\beta - 1}} + \dfrac{\beta + 3}{2^{\beta - 1}} = 1 α α ∗ λ β − w + β + λ α β − w \dfrac{1}{\alpha^{\alpha} * \lambda^{\beta - w}} + \dfrac{\beta + \lambda}{\alpha^{\beta - w}}

⟹ α + λ + w = 6 \implies \alpha + \lambda + w = \boxed{6}

The common tangent at ( 2 , 1 2 β − 1 ) (2,\dfrac{1}{2^{\beta - 1}}) is: 2 β y + ( β + 3 ) x = 2 β + 8 \boxed{2^{\beta}y + (\beta + 3)x = 2\beta + 8} .

Note: For β = 2 ⟹ a = 5 6 , b = − 55 12 \beta = 2 \implies a = \dfrac{5}{6}, b = -\dfrac{55}{12} and c = 19 3 ⟹ g ( x ) = 1 12 ( 10 x 2 − 55 x + 76 ) c = \dfrac{19}{3} \implies g(x) = \dfrac{1}{12}(10x^2 - 55x + 76) and a + b + c = 31 12 a + b + c = \dfrac{31}{12} .

The graph below shows f β ( x ) f_{\beta}(x) and g β ( x ) g_{\beta}(x) for β = 3 \beta = 3 .

For β = 3 ⟹ a = 19 36 , b = − 103 36 \beta = 3 \implies a = \dfrac{19}{36}, b = \dfrac{-103}{36} and c = 139 36 ⟹ g ( x ) = 1 72 ( 38 x 2 − 206 x + 278 ) c = \dfrac{139}{36} \implies g(x) = \dfrac{1}{72}(38x^2 - 206x + 278) and a + b + c = 55 36 a + b + c = \dfrac{55}{36} .

0 Helpful 0 Interesting 0 Brilliant 0 Confused

where did you get this problem

Nahom Assefa - 2 years, 10 months ago

Log in to reply

I created it.

When I create a problem I usually have an idea and then I see how it works out. For this problem I first did it for β = 2 \beta = 2 , then I decided to generalize it for any positive integer β \beta .

I recently posted a similar problem for β = 2 \beta = 2 below:

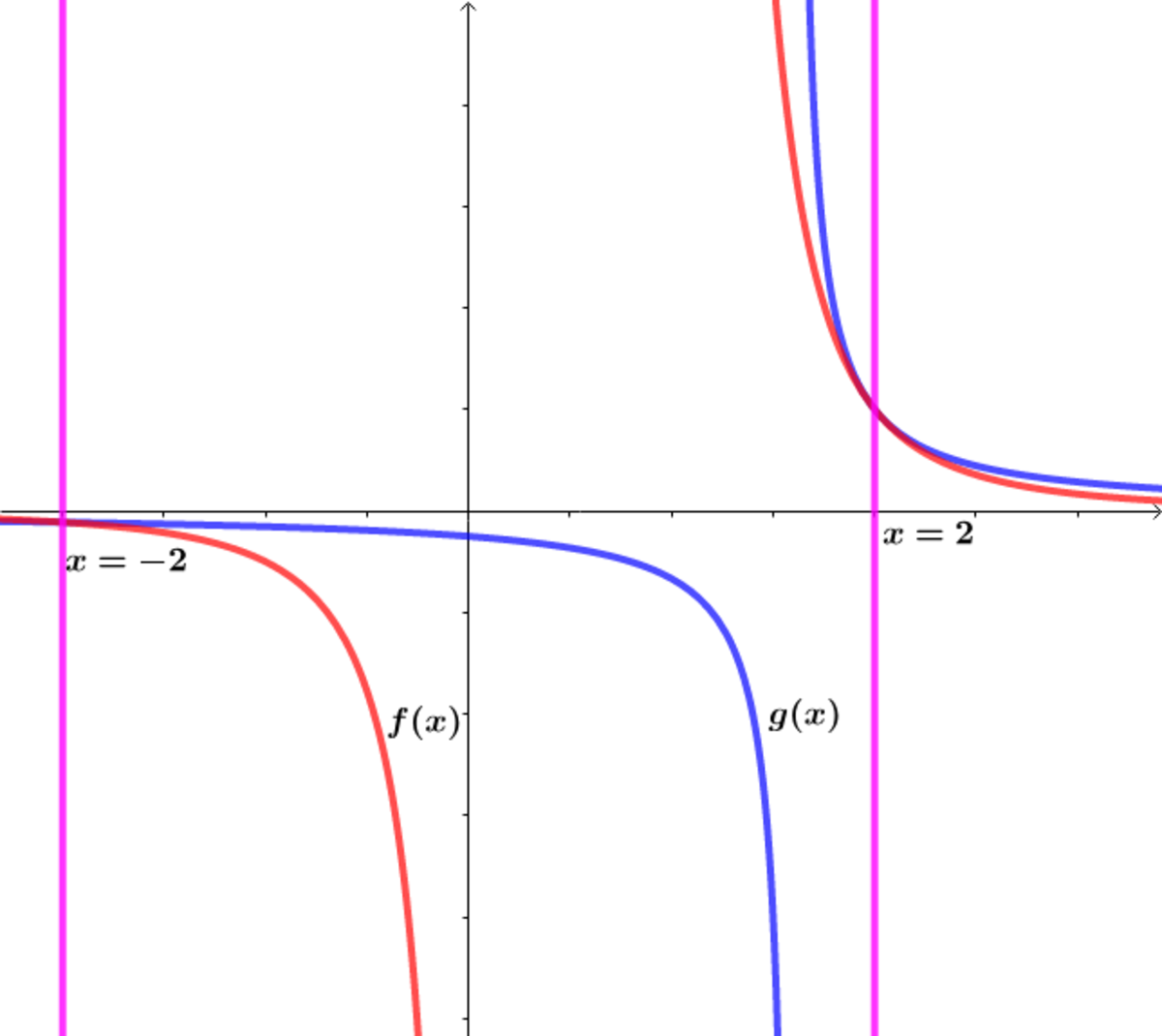
Let ∣ x ∣ > 1 |x| > 1 .

Let f ( x ) = ∑ n = 0 ∞ 1 x 3 + n − x 2 + n f(x) = \sum_{n = 0}^{\infty} \dfrac{1}{x^{3 + n} - x^{2 + n}} and g ( x ) = 1 a x + b g(x) = \dfrac{1}{ax + b} .

If g ( 2 ) = f ( 2 ) g(2) = f(2) and g ( − 2 ) = f ( − 2 ) g(-2) = f(-2) and V 1 V_{1} is the volume of the region bounded by the two curves f ( x ) f(x) and g ( x ) g(x) on [ 2 , ∞ ) [2,\infty) when revolved about the x x -axis and V 2 V_{2} is the volume of the region bounded by the two curves f ( x ) f(x) and g ( x ) g(x) on ( − ∞ , − 2 ] (-\infty,-2] when revolved about the x x -axis, find V 1 + V 2 V_{1} + V_{2} to eight decimal places.

Unfortunately, since it involved partial fractions I could not generalize it for any positive integer β \beta .

Rocco Dalto - 2 years, 10 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...