Compact Cap on Cone
Find the minimum surface area of a spherical sector which has an acute apex angle and a unit volume.
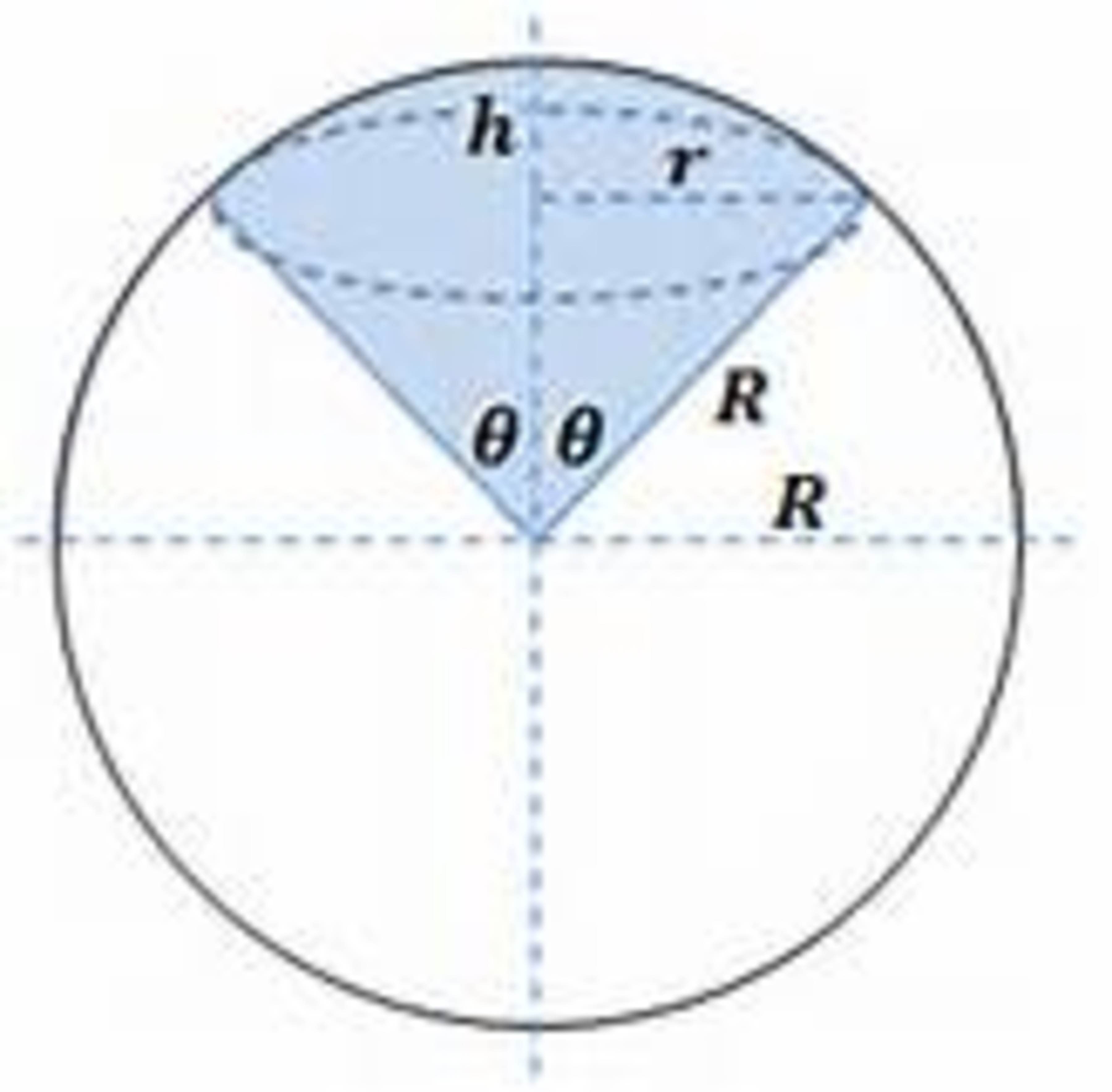
Give your answer to 3 significant figures.
Clarification: The surface area includes both the cap and the cone.
The answer is 5.61.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The volume of a spherical sector of semi-vertical angle θ and radius R is V = 3 2 π R 3 ( 1 − cos θ ) The surface area of the cap is 2 π R 2 ( 1 − cos θ ) while the cone has base radius R sin θ and slant length R , and hence surface area π R 2 sin θ . Thus we are asked to minimise A = 2 π R 2 ( 1 − cos θ ) + π R 2 sin θ subject to the constraint 3 2 π R 3 ( 1 − cos θ ) = 1 Eliminating R from these equations, we deduce that A = ( 2 9 π ) 3 1 f ( 2 1 θ ) where f ( x ) f ′ ( x ) = 2 ( sin x ) 3 2 + ( sin x ) − 3 1 cos x = 3 4 ( sin x ) − 3 1 cos x − 3 1 ( sin x ) − 3 4 cos 2 x − ( sin x ) 3 2 = 3 1 ( sin x ) − 3 4 ( 3 sin x − cos x ) ( cos x − sin x ) and hence turning points for the function f in the range 0 < x ≤ 2 1 π occur at x = tan − 1 3 1 and x = 4 1 π . It is easy to check that the first of these is a local minimum, and the second is a local maximum.
When θ = 2 tan − 1 3 1 ≈ 3 6 . 8 7 ∘ , the surface area of the sector is 5 . 6 1 1 6 5 . This is a minimum surface area for 0 < θ ≤ 2 1 π , namely for acute semi-vertical angles.
However, if we are prepared to allow the semi-vertical angle θ to be obtuse, and take values 0 ≤ θ ≤ π , then the minimum at 2 tan − 1 3 1 is no longer a global minimum. The function f ( x ) is minimized over the interval 0 < x ≤ 2 1 π at x = 2 1 π , as the below graph of f ( x ) against x shows (the minimum value is 2 ):
Thus, if we allowed obtuse semi-vertical angles, the minimum surface would be achieved at θ = π , and would therefore be the surface area of a sphere of unit volume, which would be 4 . 8 3 5 9 8 .