Compare Medians against Side Comparison
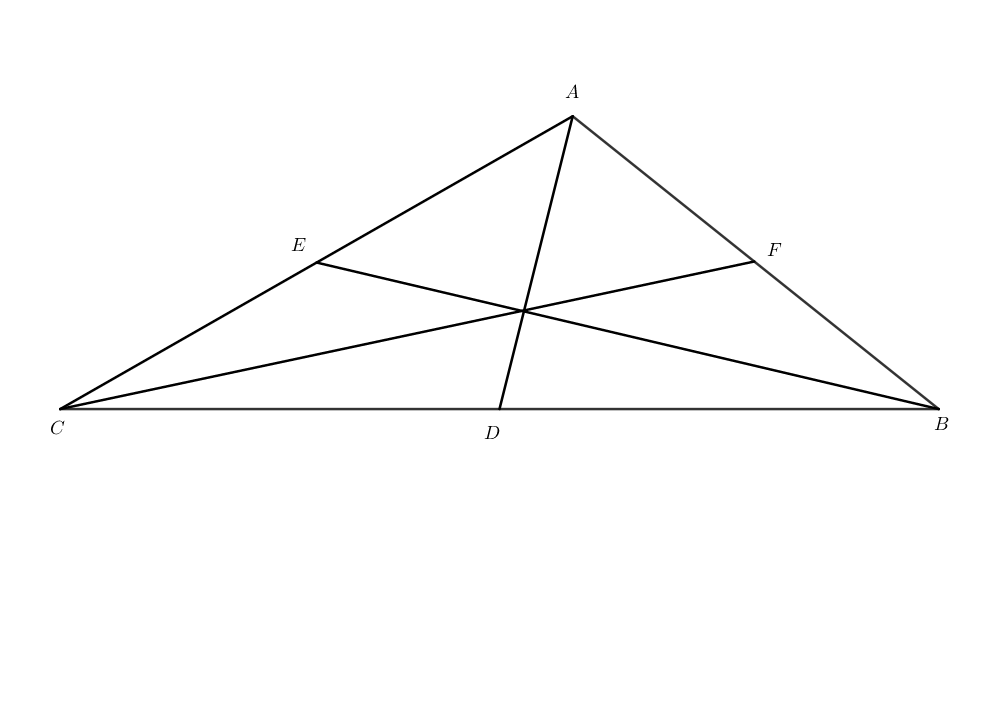
In Δ A B C ─
Sides: A B = c , C A = b , B C = a ;
Medians: A D = d , B E = e , C F = f .
Given a > b > c , which of the medians is the largest?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Why? Median doesn't mean the height of the small triangle.
Log in to reply
therefore the shorter the median the larger the sine and so the side opposed to it.
From comparison among the equal areas of triangle AMB = 2/9 d e sin(AMB) ; to area AMC = 2/9 d f sin(AMC) and to the area CMA = 2/9 f e sin(CMA). since d < e < f therefore
I will apply the Apollonius' Theorem .
By applying Apollonius' Theorem , we can have─
c 2 + b 2 = 2 ( d 2 + ( 2 a ) 2 )
⟹ c 2 + b 2 = 2 ( d 2 + 4 a 2 )
⟹ c 2 + b 2 = 2 × 4 4 d 2 + a 2
⟹ c 2 + b 2 = 2 4 d 2 + a 2
⟹ 4 d 2 = 2 ( b 2 + c 2 ) − a 2
⟹ 4 d 2 = 2 ( a 2 + b 2 + c 2 ) − 3 a 2 … … … ( I ) .
Similarly,
4 e 2 = 2 ( a 2 + b 2 + c 2 ) − 3 b 2 … … … ( I I ) .
4 f 2 = 2 ( a 2 + b 2 + c 2 ) − 3 c 2 … … … ( I I I ) .
As a > b > c , we can conclude from ( I ) , ( I I ) and ( I I I ) that
4 d 2 < 4 e 2 < 4 f 2
⟹ d < e < f .
Yes, The larger side supports the smaller median in a triangle . So, f is the answer.
Solution is obvious naming M as the point where the three medians meet. The three triangles AMB, BMC, CMA have same area therefore the smallest side base c AB in our case has to have the largest median CF.
The picture below will help to visualize the proof, just comparing areas of colored paralellograms.