How Do I Compare Their Densities?
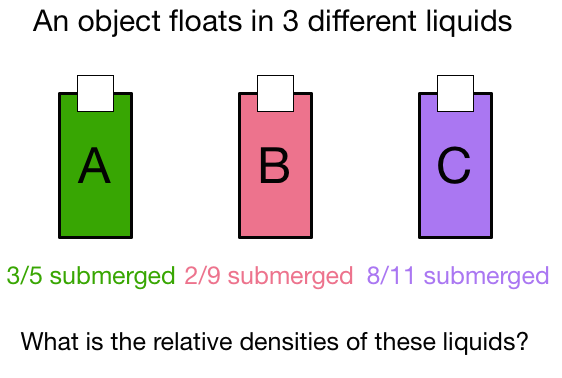
An object is put in turn , in three liquids having different densities. The object floats with parts of its volume inside the liquid surface in liquids of densities and respectively.
Which of the following gives the correct relation between and ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the total volume of the submerged body be V and let it's density be σ . Let the densities of the three liquids be ρ A , ρ B and ρ C respectively. Using Archimedes' principle and the equation of buoyancy, we get:
σ V g = 5 3 V ρ A g
and, σ V g = 9 2 V ρ B g
and also, σ V g = 1 1 8 V ρ C g
Now, solving for ρ A , ρ B and ρ C , we get:
ρ A = 3 5 σ
ρ B = 2 9 σ
ρ C = 8 1 1 σ
which shows ρ B > ρ A > ρ C