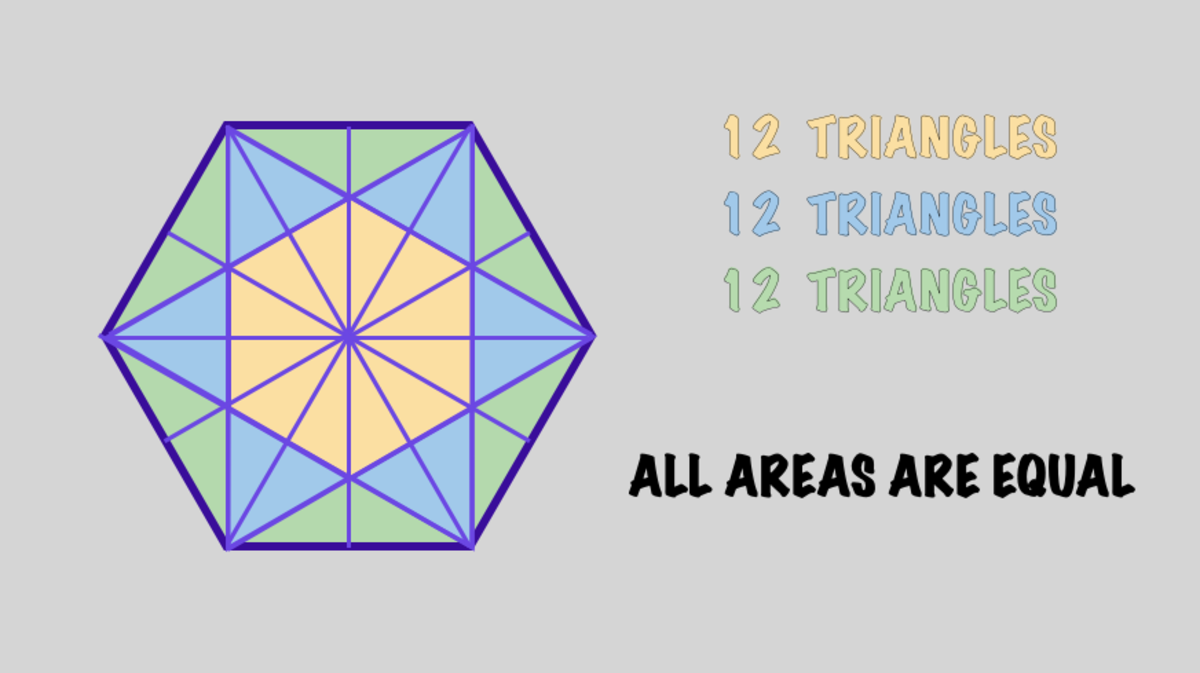
Comparing Areas ( 1 )

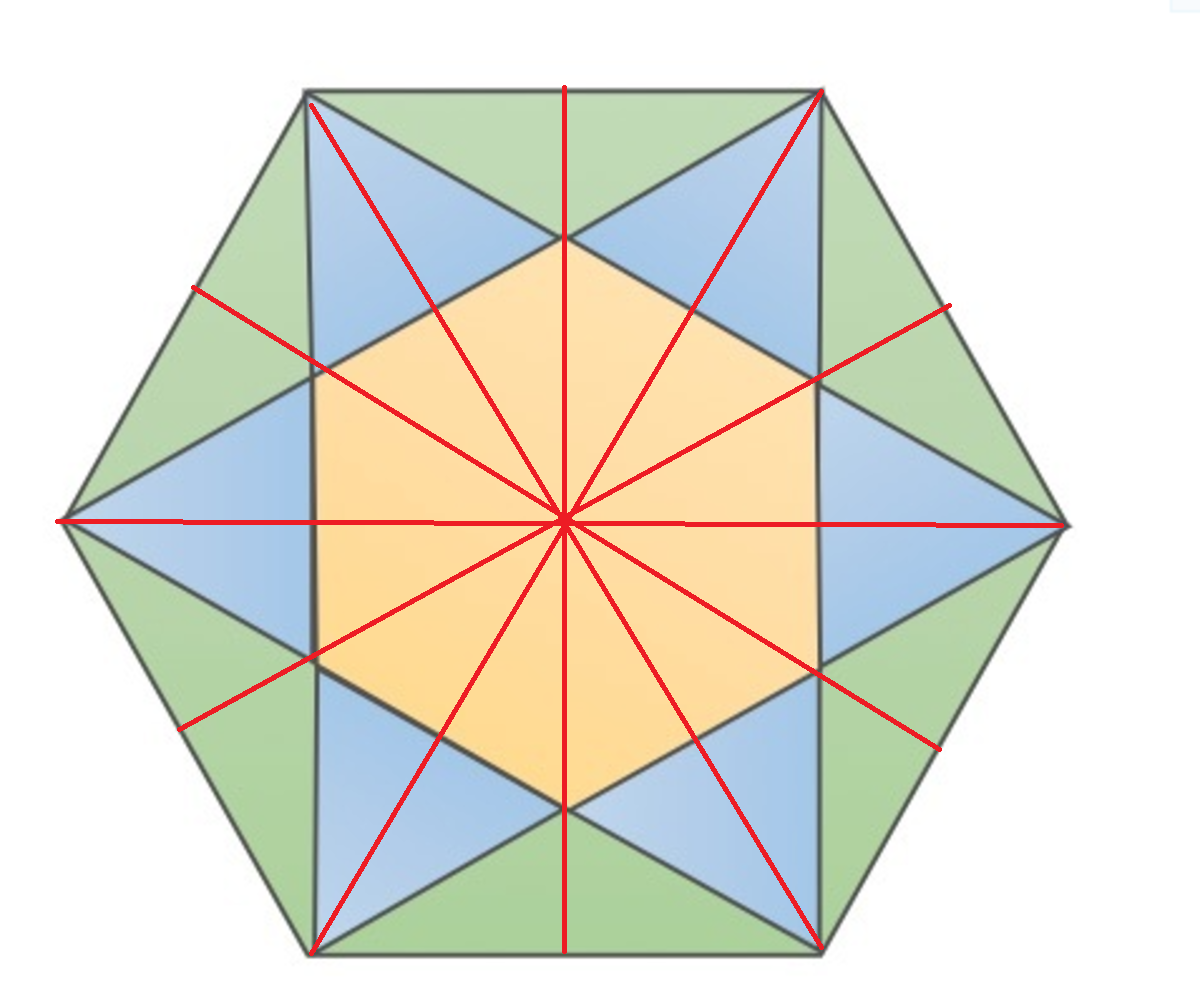Each triangle is congruent!

From the figure, we see that for $1$ green triangle, there is $1$ blue triangle and $1$ orange triangle.

Hence, All the areas are same.

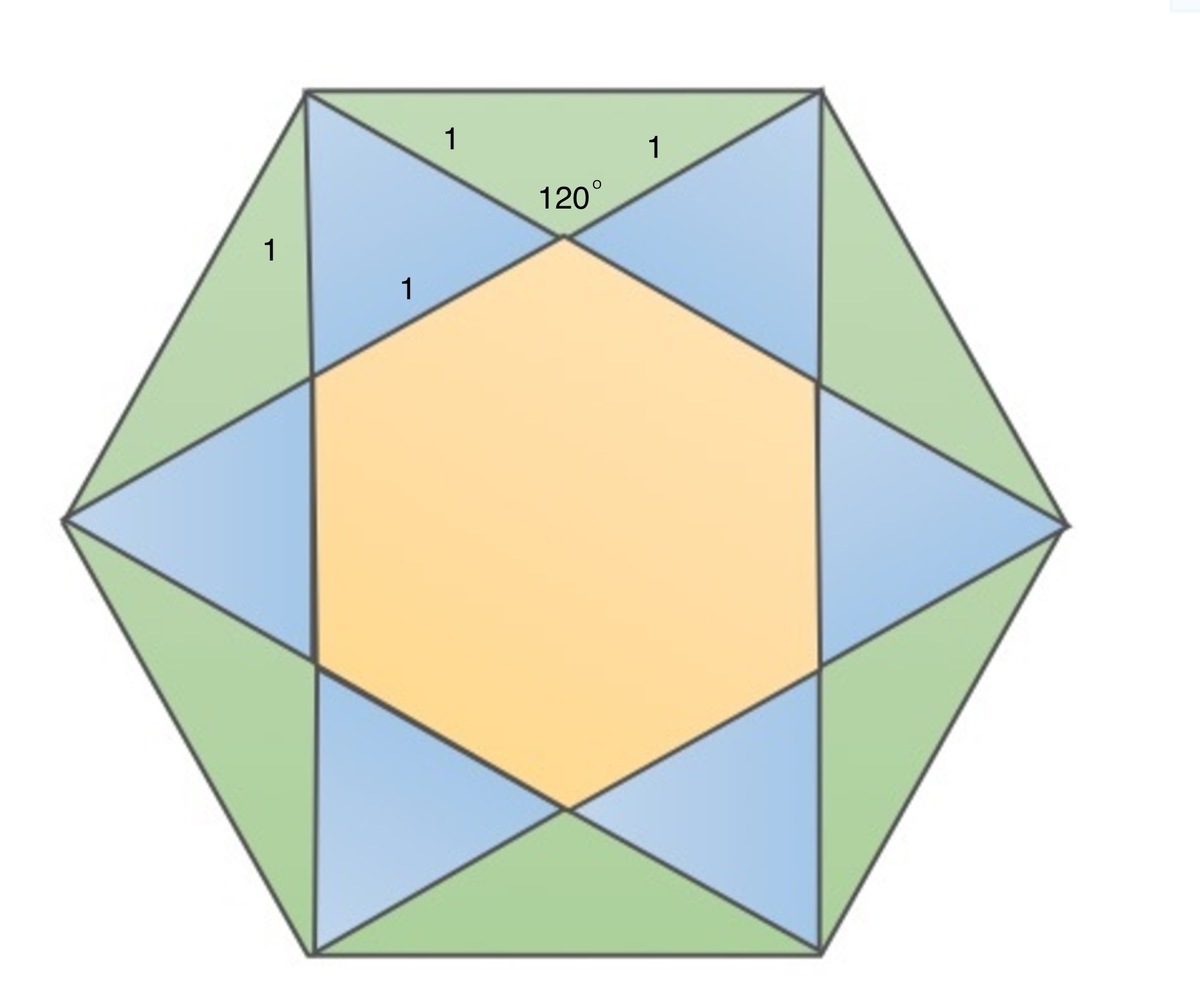
Area of one blue equilateral triangle is : $\frac{\sqrt{3}}{4}(1^2)\implies$ Area of $6$ blue triangles is: $\frac{3\sqrt{3}}{2}$

Area of the regular hexagon of side $1$ : $\frac{3\sqrt{3}}{2}$

Area of one isosceles Green triangle of non-base side $1$ is : $\underbrace{\frac{\sqrt{3}}{2}}_{\sin 120^\circ}\times\frac{1}{2}\times 1^2 =\frac{\sqrt{3}}{4} \implies$ Area of $6$ Green is : $\frac{3\sqrt{3}}{2}$

$\boxed {\text{ All Areas are Equal} }$

Formulas used: $(s=1)$

Area of an equilateral Triangle: $\frac{\sqrt{3}}{4}s^2$

Area of an Isosceles Triangle: $\frac{1}{2} s^2 \sin (120^\circ)$

Area of a regular hexagon: $\frac{3\sqrt{3}}{2}s^2$