Comparing Areas - 2

If you fold the yellow triangles along the sides of the blue square , we note that the corners of yellow square coincide with the center of the blue square and the yellow areas cover the whole blue square which can be established by simple congruence.

We can find out the length of bluesquare by Pythagoras theorem and then we can compare.

Draw the diagonals of the blue square as shown. Now observe that the blue area and the yellow area are given by: $\begin{aligned} \text{Blue Area}&=\text{Area of the 4 blue triangles}\\ \text{Yellow Area}&=\text{Area of the 4 yellow triangles} \end{aligned}$

Now observe one of the 4 congruent smaller squares formed by drawing the diagonals.

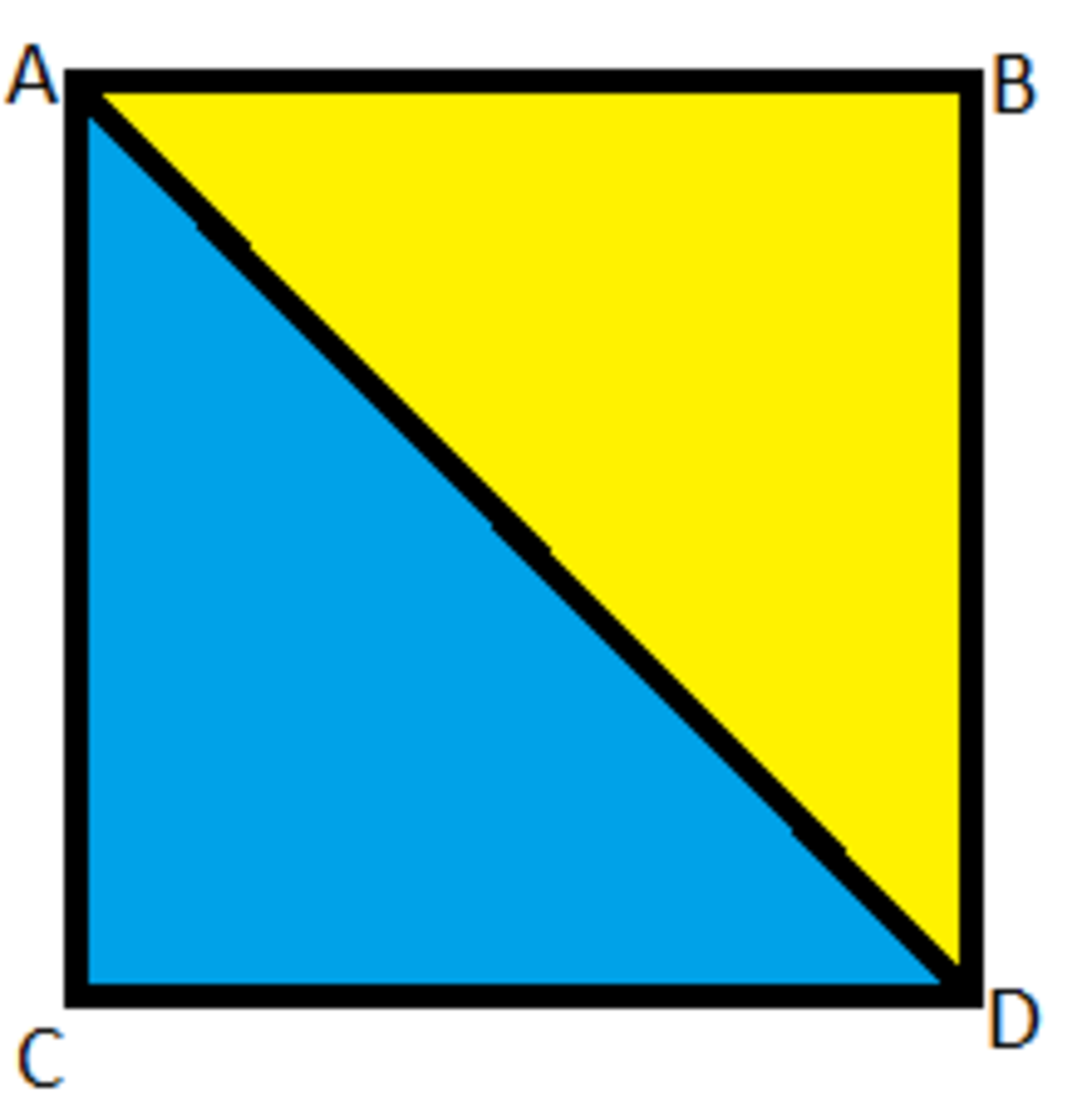
Now observe that $\overline{AC}=\overline{AB}$ , $\angle CAD=\angle DAB$ , $\overline{AD}=\overline{AD}$ .Hence by the SAS Postulate, the blue and yellow triangles are congruent.Hence: $\text{Area of the 4 blue triangles}=\text{Area of the 4 yellow triangles}\\ \implies \boxed{\text{Blue Area}=\text{Yellow Area}}$