Comparing Areas with Circles.
B is the area of the blue region, and R is the area of the red region.
Which statement is correct?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
24 solutions
Do you mean B?
Log in to reply
Yes, I must be colorblind. I must have thought it was green. Thanks.
Log in to reply
It was originally red and green- looks like they changed it for red green colourblind people
It's interesting how the areas of the overlap do not matter.
Log in to reply
The overlap would matter if the radii were not perfect squares.
Log in to reply
It matters when r r e d 1 2 + r r e d 2 2 = r b l u e 2 .
What happens if the circles are concentric?
Log in to reply
It actually still holds up if two red regions and a blue region overlapping is red (Think of it like the first red and blue produce white, and the second red turns that red).
We can split it up into two cases:
1.) Both red circles are fully inside the blue one
First, if the 3 circles are centered at the same point, then B=100pi-64pi=36pi and R=36pi , so B=R
If we move the smaller red circle around within the larger red circle, the areas certainly won't change. Similarly, moving the larger red circle (with the smaller one inside it) won't change the areas. If the smaller red circle is not fully contained within the larger one, then the red area turned white is also subtracted from the blue, and the areas stay equal.
2.) One is fully inside the blue circle, one is not fully inside
We can use similar reasoning as above, so I'll just say what you can show:
-One red circle is fully inside the blue circle, the other is tangent or not even touching it -> B=R
-Red circle on the outside has overlap with the blue circle, not the other red -> B-W=R-W
-Red circle on the outside has overlap with both the inside red and blue -> Red area gained is also taken away from the white area, meaning there is an equal gain in blue area
I proved it a different way, but this is the most general. Very good.
Generalizing Chew-Seong Cheong's solution for circles of any radii, let: the white area be W the blue area be B = pi * b^2 - W the red area be R = pi * (c^2 + d^2) - W ; assumed that the two red circles don't overlap each other
Eliminate W from the last two equations to get B / R = 1 + (pi/R) * [b^2 - (c^2 + d^2)]
That last term on the right is zero in the case presented, so it doesn't matter how big W is, as long as the two red circles don't overlap each other. Any perfect square has B = R, not just the given 5^2 = 3^2 + 4^2 b^2 = c^2 + d^2
My original solution was to notice that the overlap between the three circles would have to include three special cases: (1) W = 0 (or arbitrarily small overlap), where the circles are tangent (2) W = the area of one of the red circles, the other tangent (3) W = the area of the other red circle, the remaining one tangent
Since any of these three cases must hold, I could use the first one. In that way I reasoned that the two red circles must have area R = pi * (r1^2 + r2^2) and the blue circle must have area B = pi * b^2 so that R/B = 1
I like Chew-Seong Cheong's solution best.
Sum of Red areas before intersection is same as area of blue circle. And then after intersection equal parts are cut out from both the total red and the total blue so are net remains unchanged.
That is clean. We did not need to do any explicit computations.
Clearly, an elegant solution! Stupidly, I used algebra verifying his terse observation. James
Since the answers are all equations, the size of the white region must not matter. You might as well let the circles be tangent. Then B = 1 0 0 π and R = 6 4 π + 3 6 π = 1 0 0 π and the solution is obvious.
This would be a much better problem had it specified there must be some overlap and the choices been
B < R , B = R , B > R
Exactly! That's why the engineer and the mathematician fights in me every time I encounter a problem like this. And of course, the engineer always wins, what I sometimes dislike, sometimes not :)
That's exactly the way I did it after I realized the white spaces subtracted the same amount from the red as they did from the green.
After reviewing the other methods used I realized that they all made it way harder than it actually is. So many people read way to much into a problem because they were taught their intellect was greater than the question so they must add to the question to live up to that standing. Because the question asked about the red and green areas most assumed that you had to remove the intersections of all 4 areas to figure the remainder of the final 3. They then forget that all 4 areas were represented within the intersections before they occurred therefore.....
I agree that the problem would be better with different answers. Assuming the areas before intersection were not equal, knowing the proportion would be impossible to determine without knowing how much intersection there was.
I feel like they actually made it harder this way, making us look way too deep when the answer was actually obvious.
Let the white areas be X & Y. Then:
The red area is ( 1 6 2 × π ) + ( 1 2 2 × π ) − ( x + y ) = 4 0 0 π − ( x + y )
The blue area is ( 2 0 2 × π ) − ( x + y ) = 4 0 0 π − ( x + y )
The red area equals the blue area
You've reached the right conclusion, but might want to re-think your formula for the area of a circle. pi x r^2 not pi x d^2
Since we are not told the area of the overlap, the only solution that works for any amount is that the areas are equal! Obviously I did the 10^2 = 8^2 + 6^2 first before realizing this logic-based approach...
We can ignore the 'white' overlaps as that would be equally removed from both. What we then notice is that the diameters 20,16,12 gives us radii 10,8,6 which we might also recognize as a scalar multiple of a 3,4,5 triangle. Since area is a factor of r^2, the areas are equiv.
That was approximately my method as well. First, setting the two colored circles into an equation, I desired to factor out as much as possible: Pi Br^2 = Pi R1r^2 + Pi*R2r^2 1st: factoring out the pi in the area eqns 20^2 = 16^2 + 9^2 2nd: the common multiple of 4, leaving the 3, 4, 5 radii 5^2 = 4^2 + 3^2 3rd: squaring the radii 25 = 16 + 9 25 = 25 😃
The answer choices suggest that a proportional relationship exists between B and R no matter the configuration. Therefore, we consider the configuration where none of the circles touch. Since 1 6 2 + 1 2 2 = 2 0 2 , B = R .
This one can be solved by looking at the Pythagorean Triple 3 2 + 4 2 = 5 2 and its multiplied statement ( 4 ⋅ 3 ) 2 + ( 4 ⋅ 4 ) 2 = ( 4 ⋅ 5 ) 2 , which leads to our diameter triple { 1 2 , 1 6 , 2 0 } .
Using the area formula for the circle A = π / 4 ⋅ d 2 gives us a factored version of our diameter triple in Pythagorean form.
Just knowing d r e d 1 2 + d r e d 2 2 = d b l u e 2 shows us that: The FULL blue circle area ( B + W h i t e 1 + W h i t e 2 ) equals the FULL combined red circle areas ( R 1 + W h i t e 1 ) + ( R 2 + W h i t e 2 ) .
Combined: B + W h i t e 1 + W h i t e 2 = R 1 + W h i t e 1 + R 2 + W h i t e 2
Finally we can subtract both white regions from both sides, leading to B = R 1 + 2 .
Well I took a less common approach: since the area of the big circle and the combined area of the two smaller circles remain the same, we can be sure that (B-R) must be a constant; however it is obvious that the value of B and R can change (the position of the circles are not determined; this is also the main reason why my method works in this question). Under this situation, the only answer with the possiblilty to apply with the change of B and R is the first answer, B=R.
(Situations like B=X*R where X is positive and doesn't equals to 1 exists, but only in special conditions; plus the values of R & B would be determined)
(Also, just being nit-picking, the question could be improved by an additional note that the two red circles do not intersect with each other.)
The only way that the ratio between R and B can be independent of the white areas (constant) is if B = R. Due to the way that the question is formulated, we can deduce this without even calculating the areas, which are of course equal.
Let's star by A(r) = πr²
We can see that the red circle is missing some fancy shape. But, the blue circlesvis missing the same shape. So, we can ignore the fancy shape
(12² + 16²)π = 20²π
In conclusion the areas are equal
The white areas are subtracted from both the blue and red areas equally, so it will not matter. And the blue and red areas are equal initially without the cut. Therefore B=R.
Area of largest circle equals sum of areas of two smaller circles. Blue area is area of largest circle minus sum of white areas. Red area is sum of areas of two smaller circles minus sum of white areas. Therefore blue area equals red area
Area of a circle = π x radius^2
10 x 10 x π = 100π
6 x 6 x π = 36π
8 x 8 x π = 64π
36 + 64 = 100
The white areas are deducted from both circles equally, so they do not matter!
The distance between circle centres is not specified. If a unique solution exists then it matters not whether the white areas exist. 100 pi = (64 +36) pi.
Having said that, If the circles were concentric (which the diagram does not specifically disallow) what would the answer be?
The "white" area removes as much red as blue area, so the ratio of removed area is 1 : 1. Now notice that we don't have any exact measurement of the white area. There is no way to calculate this. Than it must not matter for this problem. The only reasonable answer is thus B = R. The ratio R : B must be 1 : 1. Every other ratio would be changed if we change how far we would "slide the circle in" (resulting in an increase of white are).
Let's give an example to make the last statement more clear. Let's say B = 1.5R. If R = 10 than B = 15. Removing a little white area (let's remove an amount of 5) would result in R = 5 and B = 10. This means that B = 2R, clearly the ratio B : R has changed.
12,16,20 are the numbers of right angle triangle. 1 2 2 + 1 6 2 = 2 0 2 so R = B
Note that the diagram is not very specific, so you can move the circles. Note that a change in the white region changes both the blue and red regions by the same amount, so we move both the red circles outside of the blue region. Now the area of the red region is ( 1 2 2 + 1 6 2 ) π = 4 0 0 π and the area of the blue region is 2 0 2 π = 4 0 0 π . So, B = R .
I figured since the degree of overlap doesn't seem to matter, set it to 0 and you're home free
Kudos to all the 'engineering' solutions.
But I like the good old inclusion exclusion.
Let A be the total area
A1 be area of the top circle, A2, be the area of the middle circle, and A3 be the area of the bottom circle.
A = A1 + A2 + A3 - (A1 ∩ A2 + A2 ∩ A3) (the other terms A1∩A3 and A1∩A2∩A3 are 0 here since the top and bottom circles don't intersect) 1) Now if we observe, A2 - (A1 ∩ A2 + A2 ∩ A3) is A(Green)
So A = A1 + A3 + A(Green) = 100π + A(Green)
2) Also, A1 - (A1 ∩ A2) + A3 - (A2 ∩ A3) is A(Red)
so A = A2 + A(Red) = 100π + A(Red)
From 1) and 2) we get A(Green) = A(Red)
I think it related to the Pythagorean theorem. $12^2 + 16^2 = 20^2$
I worked it out as follows: 1)The blue area is most of a circle with total area 100pi and the red area is most of two circles whose combined area adds up to 100pi (64pi + 36pi). 2)Both the red and blue areas are reduced from 100pi by the same amount (the white area). 3)Therefore the red and blue areas are equal.
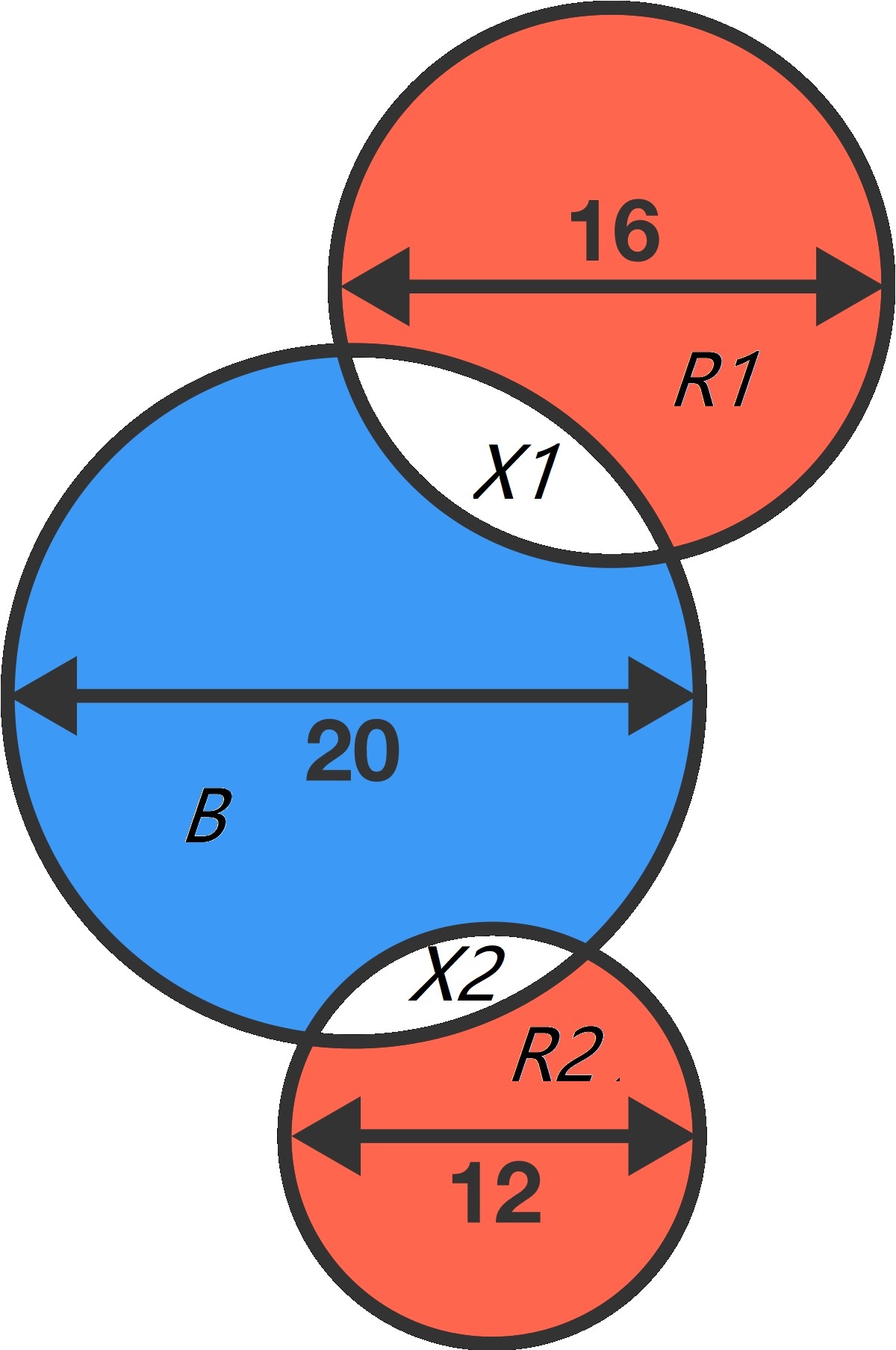
From the graph, one can get
⎩ ⎪ ⎨ ⎪ ⎧ B + X 1 + X 2 = 1 0 0 π 6 4 π = R 1 + X 1 3 6 π = R 2 + X 2
Adding these three equations together, get you B = R .
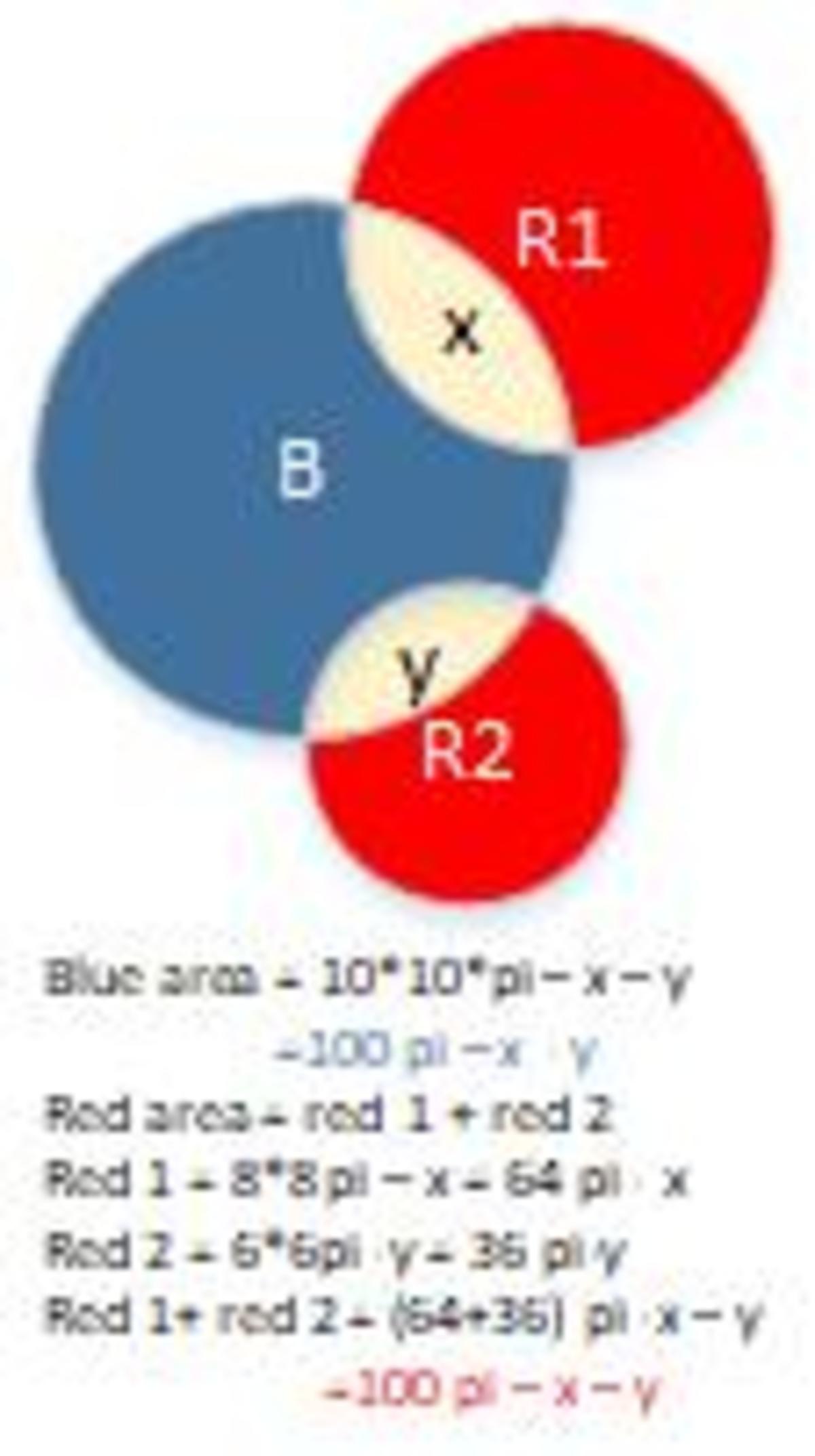
Let the area of the two white regions together be W . Then B = 1 0 2 π − W = 1 0 0 π − W and R = 8 2 π + 6 2 π − W = 1 0 0 π − W . Implying that B = R .