Area with Lunar Moons (2)
Geometry
Level
pending
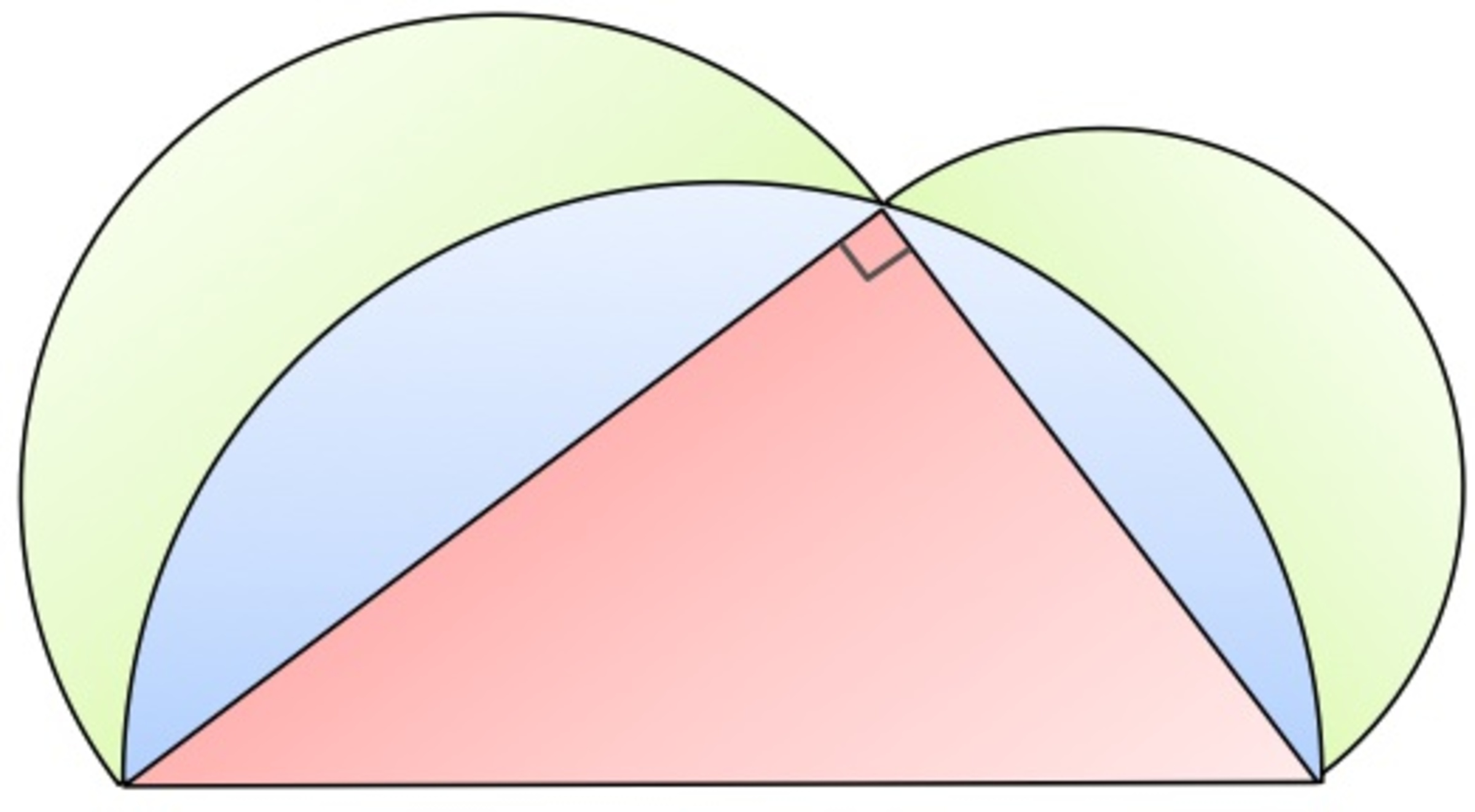
Three semi circles are constructed on the legs and hypotenuse of a right triangle. Compare the green area (G) to the red area (A). what do you notice?
G > R
The relationship can't be determined.
G < R
G = R
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
If the legs of the triangle are a and b , then the area of the lunes is the two semicircles, 2 π a 2 + 2 π b 2 , plus the triangle 2 a b , minus the white semicircle 2 π c 2
But 2 π a 2 + 2 π b 2 + 2 a b − 2 π c 2 = 2 π ( a 2 + b 2 − c 2 ) + 2 a b = 2 π × 0 + 2 a b = 2 a b