Comparing Inside and the outside

Geometry Level 3

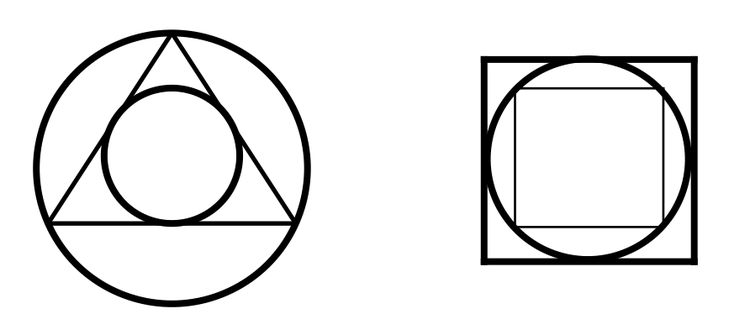Above shows two figures. The one on the left shows a circumcircle and an incircle of an equilateral triangle. The ratio of their areas is 4.

The one on the right shows a circumcircle and an incircle of a unit square. The ratio of their areas is 2.

Now consider a $n$ -sided regular polygon. Let the area of a circle inscribed in the regular polygon be $A_n$ . And let the area of a circle circumscribed the regular polygon with be $B_n$ . Evaluate

$\lim_{n\to\infty} \frac{B_n}{A_n}$

1.50

1.25

1.75

1.00

1 solution

Timothy Wan
Jun 19, 2015

An n-sided polygon has n corners touching the circle.As n goes to infinity,there are infinite corners touching the circle. Therefire,the n-sided figure is the circle at n=infinity. Thus the area is the same,and $A_n/B_n=1$

Comparing Inside and the outside

1 solution

0 pending reports