Complete the Square Grid!
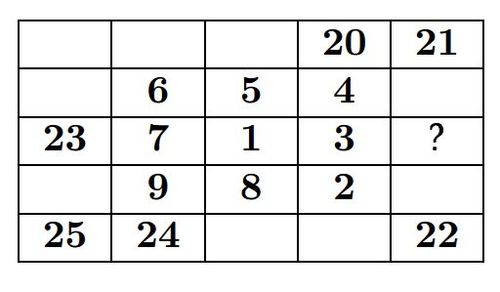 In the diagram given above, the numbers from 1 to 25 are to arranged in a
square grid so that each number except 1 and 2, is the sum of two of its
neighbours
. Some of the numbers have already been filled in. Which number must replace the "
" when the grid is complete.
In the diagram given above, the numbers from 1 to 25 are to arranged in a
square grid so that each number except 1 and 2, is the sum of two of its
neighbours
. Some of the numbers have already been filled in. Which number must replace the "
" when the grid is complete.
Note - Numbers in the grid are neighbours if their squares touch along a side or at a corner. For example: the number "1" has eight neighbours , the number "21" has three neighbours .
Bonus - Complete the Grid.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The solved grid would be