Complex CUBEROOTs of UNITY.
We Know that solutions of "
= 1" are commonly called the cube roots of unity.
This equation has one real solution, z = 1, but it also has two complex solutions.
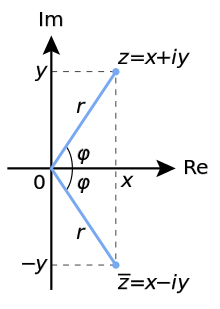
The complex number (x + iy) can be represented by a vector in the complex plane, as shown in Figure.
The Cube Roots of Unity when represented on Argand Diagram form the vertices of ..............
Image Credit Wikipedia
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Solution