Complex Current Divider
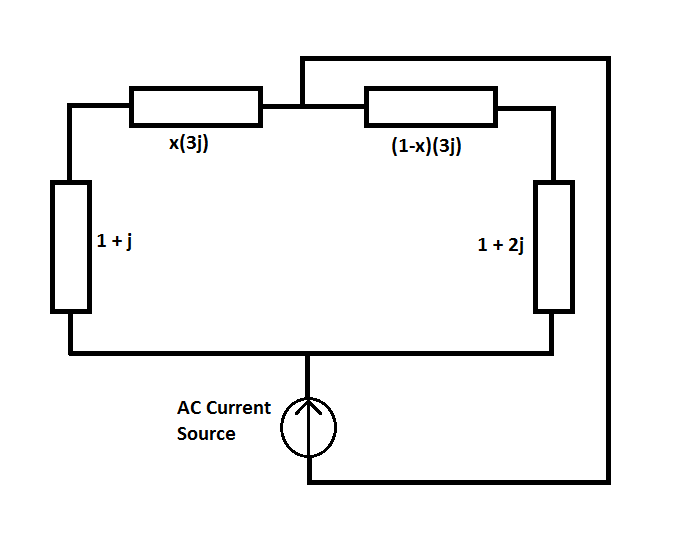
An AC current source feeds a circuit with the complex impedances shown in the diagram. The circuit acts as a current divider, with part of the injected current flowing through the left branch and part of it flowing through the right branch.
If the currents in the left and right branches are perfectly in-phase with each other, determine the value of x (to 2 decimal places).
Clarification: x is a positive real number. The symbol j denotes the imaginary unit .
The answer is 0.67.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let the left and right impedances be Z 1 , 2 , respectively. They both consist of a series connection: Z 1 Z 2 = ( 1 + j ) + x ( 3 j ) = 1 + j ( 1 + 3 x ) = ( 1 + 2 j ) + ( 1 − x ) ( 3 j ) = 1 + j ( 5 − 3 x ) ⇒ ⇒ ∢ ( Z 1 ) ∢ ( Z 2 ) = arct g 2 ( 1 + 3 x , 1 ) = arct g 2 ( 5 − 3 x , 1 ) Let I 1 , 2 be the currents through Z 1 , 2 from bottom to top, respectively. Then we get via current divider: I 1 = Z 1 Z 2 ⋅ I 2 = ∣ ∣ ∣ ∣ Z 1 Z 2 I 2 ∣ ∣ ∣ ∣ e j ( ∢ ( Z 2 ) − ∢ ( Z 1 ) + ∢ ( I 2 ) ) ⇒ ∢ ( I 1 ) = ∢ ( Z 2 ) − ∢ ( Z 1 ) + ∢ ( I 2 ) If both current phases ∢ ( I 1 , 2 ) are equal (mod 2 π ), we can solve for x : k ∈ Z : ∢ ( I 1 ) = ∢ ( I 2 ) + 2 π k ⇒ ∢ ( Z 2 ) = ∢ ( Z 1 ) + 2 π k ⇒ 1 + 3 x = 5 − 3 x ⇒ x = 3 2 ≈ 0 . 6 6 7
Since both paths are in phase, I looked for a value of x that would give both paths the same complex impedance. When you add up the impedances of the path on the left and the path on the right you find that both paths have a real part of "1". You just need to equate the expressions for the imaginary parts, which gives you a value of x = 3 2