Complex Cyclic Cystems

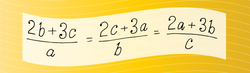Let $k$ be the complex number such that $\frac{2b+3c}{a}=\frac{2c+3a}{b}=\frac{2a+3b}{c}=k,$ then $\begin{aligned} 2b+3c&=ak \\ 2c+3a&=bk \\ 2a+3b&=ck, \end{aligned}$ adding the equations we get $5(a+b+c)=k(a+b+c)$ .

1) If $a+b+c\neq 0$ then $k=5$ , and solving the linear equations we easily obtain $a=b=c$ . Thus one value of $\left|\frac{5a^2+5b^2}{c^2}\right|$ is 10.

2) If $a+b+c=0$ , since $a\neq0$ and $b\neq 0$ there exists a non-zero $\lambda \in \mathbb{C}$ such that $b=\lambda a$ , then $c=(-1-\lambda) a$ . Replacing in $\frac{2b+3c}{a}=\frac{2c+3a}{b}$ we get $\begin{aligned} \frac{2\lambda a+3(-1-\lambda)a}{a}&=\frac{2(-1-\lambda)a+3a}{\lambda a} \\ \frac{-3-\lambda}{1}&=\frac{1-2\lambda}{\lambda} \\ -3\lambda-\lambda^2&=1-2\lambda \\ 0&=\lambda^2+\lambda+1 \end{aligned}$ Then $\lambda=\omega$ or $\lambda=\omega^2$ , where $\omega$ is the primitive third root of unity. Hence, in this case, we have the solutions $(a, \omega a, \omega^2a )$ and $(a, \omega^2 a, \omega a )$ .

Finally, if $(a,b,c)=(a, \omega a, \omega^2a )$ then $\left|\frac{5b^2+5c^2}{a^2}\right|=\left|\frac{5\omega^2a^2+5\omega^4a^2}{a^2}\right|=\left|\frac{5\omega^2a^2+5\omega a^2}{a^2}\right|=|5\omega^2+5\omega|=|-5|=5.$ Analogously, if $(a,b,c)=(a, \omega^2 a, \omega a )$ we get $\left|\frac{5b^2+5c^2}{a^2}\right|=5$ .

Therefore, the sum of all possible values of $\left|\frac{5b^2+5c^2}{a^2}\right|$ is $10+5=15$ .