Complex Distances are not so Complicated
All complex numbers z = x + i y , satisfying ∣ z − i ∣ + ∣ z + i ∣ = 4 , form an ellipse in the form A x 2 + B y 2 = C , where A , B , and C are positive integers with A and B being coprime integers. What is A + B + C ?
Notation: i = − 1 denotes the imaginary unit .
The answer is 19.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
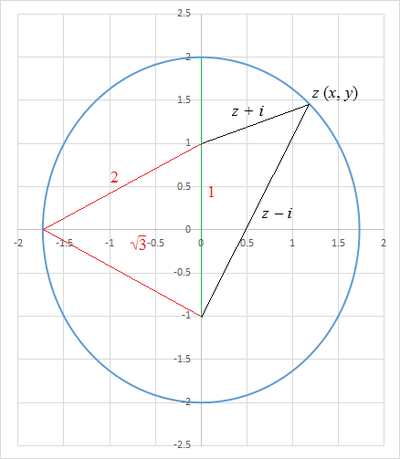 The equation
∣
z
−
i
∣
+
∣
z
+
i
∣
=
4
means that the sum of distances from point
z
(
x
,
y
)
to the two points
(
0
,
−
1
)
and
(
0
,
1
)
is equal to 4, a constant. The means that the locus of
z
(
x
,
y
)
is an ellipse with points
(
0
,
−
1
)
and
(
0
,
1
)
as the foci. The standard equation of an ellipse is
a
2
x
2
+
b
2
y
2
=
1
. Putting
x
=
0
, we find the semiminor axis
a
=
2
2
−
1
2
=
3
. Putting
y
=
0
, the semimajor axis
b
=
2
. Therefore, we have:
The equation
∣
z
−
i
∣
+
∣
z
+
i
∣
=
4
means that the sum of distances from point
z
(
x
,
y
)
to the two points
(
0
,
−
1
)
and
(
0
,
1
)
is equal to 4, a constant. The means that the locus of
z
(
x
,
y
)
is an ellipse with points
(
0
,
−
1
)
and
(
0
,
1
)
as the foci. The standard equation of an ellipse is
a
2
x
2
+
b
2
y
2
=
1
. Putting
x
=
0
, we find the semiminor axis
a
=
2
2
−
1
2
=
3
. Putting
y
=
0
, the semimajor axis
b
=
2
. Therefore, we have:
a 2 x 2 + b 2 y 2 3 x 2 + 4 y 2 4 x 2 + 3 y 2 = 1 = 1 = 1 2 Multiply both sides by 1 2 .
Therefore, A + B + C = 4 + 3 + 1 2 = 1 9 .
Nice - I didn't know an ellipse was this easily determined.
∣ x + i y − i ∣ + ∣ x + i y + i ∣ = 4 x 2 + ( y − 1 ) 2 + x 2 + ( y + 1 ) 2 = 4 x 2 + y 2 + 1 + x 2 + ( y − 1 ) 2 x 2 + ( y + 1 ) 2 = 8 [ x 2 + ( y − 1 ) 2 ] [ x 2 + ( y + 1 ) 2 ] = [ 7 − ( x 2 + y 2 ] 2 x 4 + x 2 ( y + 1 ) 2 + x 2 ( y − 1 ) 2 + ( y − 1 ) 2 ( y + 1 ) 2 = 4 9 − 1 4 ( x 2 + y 2 ) + x 4 + 2 x 2 y 2 + y 4 2 x 2 y 2 + 2 x 2 − 2 y 2 + 1 = 4 9 − 1 4 ( x 2 + y 2 ) + 2 x 2 y 2 1 6 x 2 + 1 2 y 2 = 4 8 4 x 2 + 3 y 2 = 1 2 ∴ A + B + C = 1 9
The center of the ellipse is the midpoint of the two foci, which in this case is the origin; also, the two foci lie on the y-axis, so the ellipse will have a vertical major axis.
Then the equation of the ellipse will be a 2 x 2 + b 2 y 2 = 1 , with b > a .
Let 2 c be the distance between the two foci. Then for an ellipse with a vertical major axis, it is always true for any point on the ellipse that the sum of the distances to the two focal points is 2 b , and also that b 2 = a 2 + c 2 . Thus 2 b = 4 ⟹ b = 2 , and then c = 1 ⟹ 2 2 = a 2 + 1 2 ⟹ a = 3 .
Thus the equation of the ellipse is 3 x 2 + 4 y 2 = 1 , i.e. 4 x 2 + 3 y 2 = 1 2 , and our answer is 4 + 3 + 1 2 = 1 9