Complex ellipse
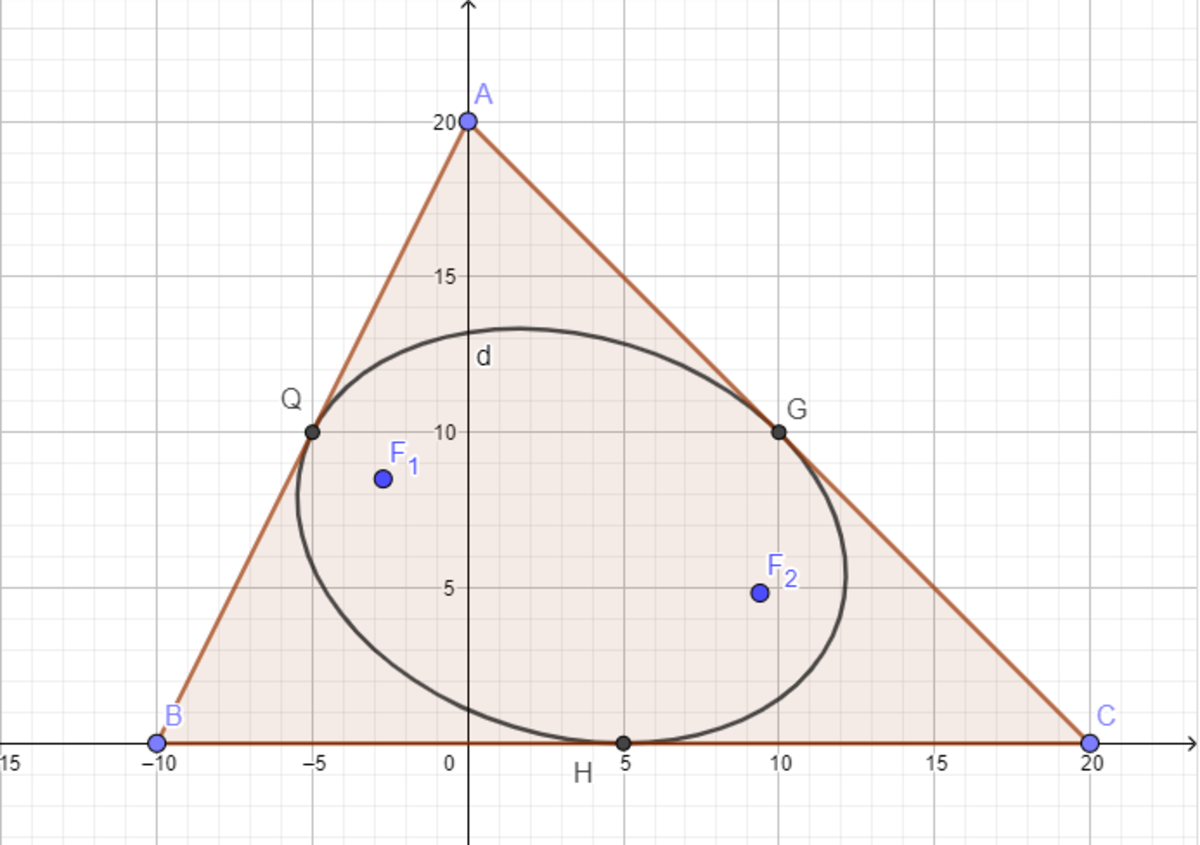
A triangle has its vertices at A ( 0 , 2 0 ) , B ( − 1 0 , 0 ) , and C ( 2 0 , 0 ) , as shown in the figure above. An ellipse can be inscribed in △ A B C such that it is tangent at the three midpoints of the sides.
If F 1 and F 2 are the ellipse foci, then ∣ F 1 F 2 ∣ 2 = C A B , where A and C are positive coprime integers and B is square-free. Find A + B + C .
The answer is 422.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Such an ellipse is called Steiner inellipse and its semi-major and semi-minor axes are given by:
a s , b s = 6 1 a 2 + b 2 + c 2 ± 2 Z
where a , b , and c are the side lengths of the triangle and Z = a 2 + b 2 + c 2 − a 2 b 2 − b 2 c 2 − c 2 a 2 .
From A ( 0 , 2 0 ) , B (-10,0)), and C ( 2 0 , 0 ) , we have a 2 = 9 0 0 , b 2 = 8 0 0 , c 2 = 5 0 0 , Z = 1 0 0 1 3 , and a 2 , b s = 6 2 2 0 0 ± 2 0 0 1 3 . Then we have:
∣ F 1 F 2 ∣ ∣ F 1 F 2 ∣ 2 = 2 a s 2 − b s 2 = 4 ( a s 2 − b s 2 ) = 4 × 3 6 2 2 0 0 + 2 0 0 1 3 − 2 2 0 0 + 2 0 0 1 3 = 9 4 0 0 1 3
Therefore, A + B + C = 4 0 0 + 1 3 + 9 = 4 2 2 .
Can you derive the formulae you mentioned?
Log in to reply
I would not like to. If you want to try, I would suggest to consider the sum of distances of the three midpoints from the two foci are the same, which is 2 a , where a is the semi-major axis. Let the coordinates of the two foci be x 1 . y 1 and x 2 , y 2 . Then we will have three equations for four unknowns but we have the additional fact that the center of the ellipse is the midpoint between the two foci.
Marden's theorem
f ( z ) = ( z − z A ) ( z − z B ) ( z − z C )
f ′ ( z ) = ( ( z − 2 0 − 0 i ) ( z + 1 0 + 0 i ) ( z − 2 0 i ) ) ′ = 0
3 z 2 − ( 2 0 + 4 0 i ) z − ( 2 0 0 − 2 0 0 i ) = 0
F 1 = 3 1 0 ( ( 1 + 2 i ) + 3 − 2 i )
F 2 = − 3 1 0 ( ( − 1 − 2 i ) + 3 − 2 i
∣ ∣ 3 1 0 ( ( 1 + 2 i ) + 3 − 2 i ) + 3 1 0 ( ( − 1 − 2 i ) + 3 − 2 i ) ∣ 2 = 9 4 0 0 1 3