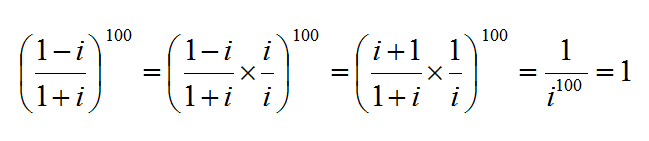Complex Mania-II
(
1
+
i
1
−
i
)
1
0
0
If the expression above equals
a
+
i
b
for real numbers
a
and
b
,then find the value of
a
+
b
.
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
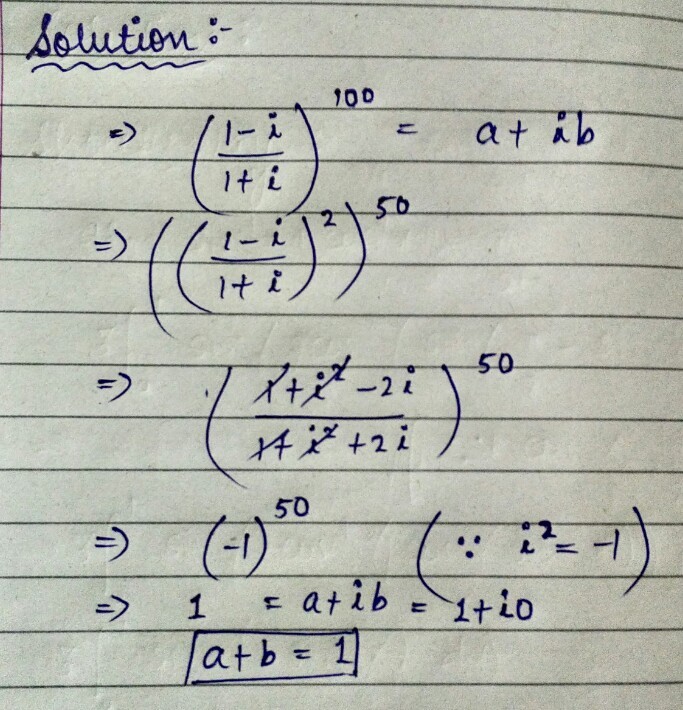
Moderator note:
That's right. Another way is to express 1 ± i = 2 ( 2 1 ± 2 i ) to polar coordinates then apply De Moivre's Theorem.
Bonus question : What would the answer be if we replace the number 100 by 99 instead?
1 + i 1 − i = ( 1 + i ) ( 1 − i ) ( 1 − i ) ( 1 − i ) = 1 − i 2 1 − 2 i + i 2 = 2 − 2 i = − i ⇒ ( − i ) 9 9 = ( − 1 ) i 3 = i ⇒ a + b = 1
In fact the possible values of a + b = { − 1 , 1 } . Because ( − i ) n = { − i , − 1 , i , 1 } congruence mod 4.
1 + i 1 − i = ( 1 + i ) ( 1 − i ) ( 1 − i ) ( 1 − i ) = 1 − i 2 1 + i 2 − 2 i
= 1 + 1 1 − 1 − 2 i = − i
( − i ) 1 0 0 = 1 (even power of any -ve number is +ve))
1 can be written as 1 + i 0 where a + b = 1 + 0 = 1
It'll be -2i instead of +2i. And hence the result will be -i. But yet it'll give the final result 1.
There's a mistake Siddharth Singh You wrote − i 1 0 0 = 1 .That is incorrect.Because: ( − a ) 2 n = a 2 n BUT − a 2 n = − 1 × a 2 n See what I'm talking about? You see, − i 1 0 0 = 1 because − i 1 0 0 = − 1 × i 1 0 0 = − 1 × 1 = − 1 . I 've corrected it.So, no need to worry.
First learn and then teach Siddharth Singh