This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Same solution as mine
( 1 − i ) 2 0 0 9 × i 2 0 0 9 ( 1 + i ) 2 0 1 1 × i 2 0 0 9 = ( ( 1 − i ) × i ) 2 0 0 9 ( 1 + i ) 2 0 1 1 × i 2 0 0 9 = ( i + 1 ) 2 0 0 9 ( 1 + i ) 2 0 1 1 × i 2 0 0 9 = ( 1 + i ) 2 × ( ( i 2 ) 2 ) 5 0 2 × i = ( 1 + 2 i + i 2 ) × i = − 2 (since i 2 = − 1 )
There's no comment section, so I'm forced to post a comment here. It is not a valid explanation but a question. I believe I've solved the problem illegitimately and I'd like to know whether I'm right to be suspicious, and also why it worked.
I started working on the problem right after reading the wiki section about powers of i, so I tried to apply what I had just read.
To simplify larger powers of i, take the last two digits of the number and divide it by 4. Find the remainder and if the remainder is k, then the value is i k
Then I commited something horrible: I ignored the fact that the problem has (1+i) and (1-i) instead of i's only and simplified it like so: ( 1 − i ) 2 0 0 9 ( 1 + i ) 2 0 1 1 = ( 1 − i ) 1 ( 1 + i ) 3 = 1 − i ( 1 + i ) 2 ( 1 + i ) = 1 − i 2 i ( 1 + i ) = 1 − i 2 i + 2 i 2 = 1 − i − 2 + 2 i = 1 − i − 2 ( 1 − i ) = − 2
I think I shouldn't have simplified the exponents, because I wasn't working with pure i's, but I'm surprised that it worked anyway. Why?
What's the problem with having a non-pure i's?
I first found out the logarithm of the given expression to the base e and then raised e to the power of the result.
lo g ( 1 − i ) 2 0 0 9 ( i + 1 ) 2 0 1 1 = 2 0 1 1 lo g ( 1 + i ) − 2 0 0 9 lo g ( 1 − i ) Now, using The principal value of lo g z = lo g ∣ z ∣ + i a r g ( z ) , where arg(z) is the principal argument of z (which is also known as its amplitude), we get,
lo g ( 1 + i ) = lo g 2 + i ( 4 π ) and l o g ( 1 − i ) = lo g 2 − i ( 4 π ) .
Substituting these values in the first equation, we get
lo g ( 1 − i ) 2 0 0 9 ( 1 + i ) 2 0 1 1 = 2 0 1 1 ( lo g 2 + i 4 π ) − 2 0 0 9 ( lo g 2 − i 4 π ) = 2 lo g 2 + 4 0 2 0 i 4 π = lo g 2 + 1 0 0 5 i π
To get the value of original expression, we raise e to the power of lo g 2 + 1 0 0 5 i π .
∴ e lo g 2 + 1 0 0 5 i π = e lo g 2 × e 1 0 0 5 i π = 2 [ cos ( 1 0 0 5 π ) + i sin ( 1 0 0 5 π ] … Using Euler’s Identity = 2 [ − 1 + i ( 0 ) ] = − 2 Feel free to comment on this solution and I apologise for any mistakes in LaTex as I am new to it.
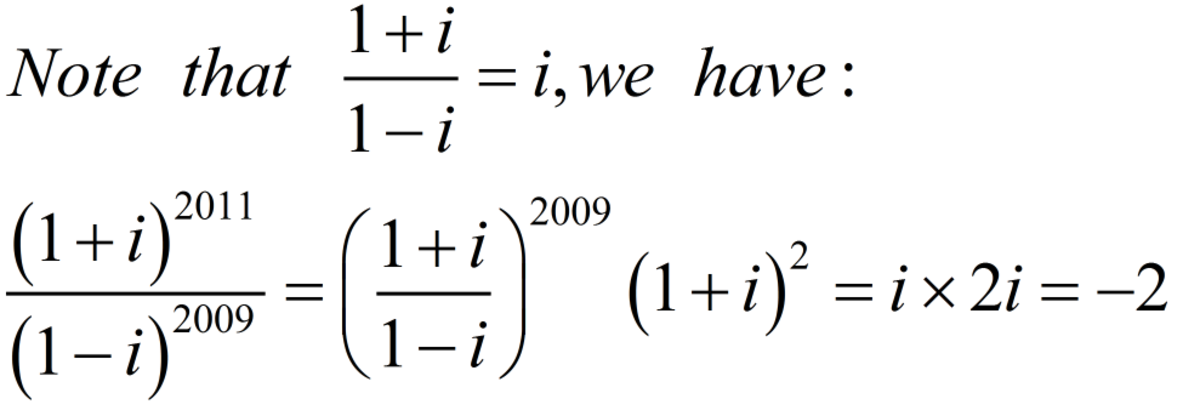
( 1 − i ) 2 0 0 9 ( 1 + i ) 2 0 1 1 = ( 1 − i ) 2 × 1 0 0 4 + 1 ( 1 + i ) 2 × 1 0 0 5 + 1 = ( − 2 i ) 1 0 0 4 ( 1 − i ) ( 2 i ) 1 0 0 5 ( 1 + i ) = ( − 2 ) 1 0 0 4 i 4 × 2 5 1 ( 1 − i ) 2 1 0 0 5 i 4 × 2 5 1 + 1 ( 1 + i ) = 1 − i 2 i ( 1 + i ) = 1 − i 2 ( i − 1 ) = − 2 Note that ( 1 ± i ) 2 = ± 2 i and i 2 = − 1 ⟹ i 4 = 1
Or using Euler's formula : e i x = cos x + i sin x .
( 1 − i ) 2 0 0 9 ( 1 + i ) 2 0 1 1 = ( 2 ( 2 1 − 2 i ) ) 2 0 0 9 ( 2 ( 2 1 + 2 i ) ) 2 0 1 1 = ( 2 ( cos 4 π − i sin 4 π ) ) 2 0 0 9 ( 2 ( cos 4 π + i sin 4 π ) ) 2 0 1 1 = ( 2 e − 4 π i ) 2 0 0 9 ( 2 e 4 π i ) 2 0 1 1 = ( 2 ) 2 0 1 1 − 2 0 0 9 e 4 2 0 1 1 + 2 0 0 9 π i = ( 2 ) 2 e 1 0 0 5 π i = 2 ( − 1 ) 1 0 0 5 = − 2 Note that e π i = − 1