Complex sine
Which of the following is a solution to sin x = 2 in the complex numbers?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions

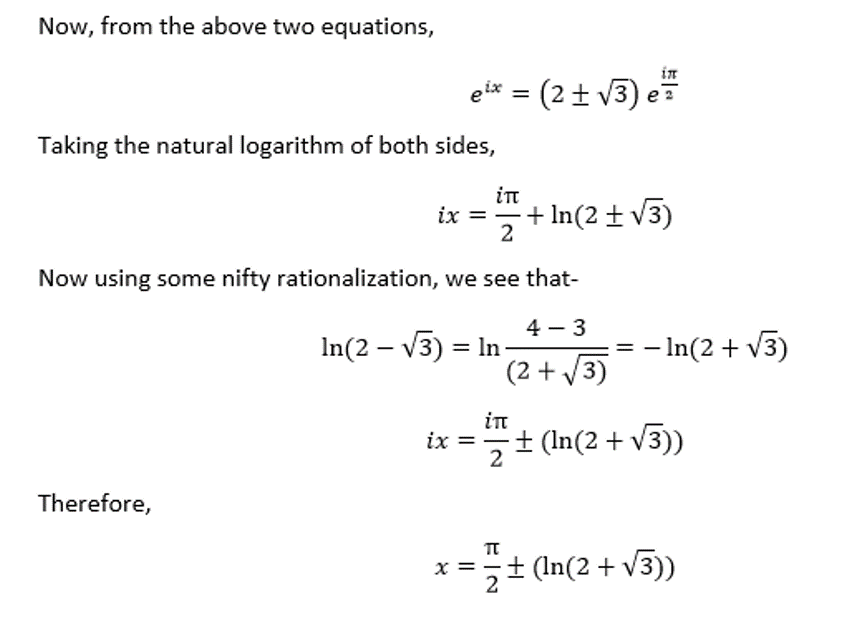
Why we can't take z = r.cisx = 2i±√3i , which is more general form of a complex number
Here's a really lazy method. In the example we already get the solution for cos x = 2 , which is x = 2 k π ± ln 2 ± 3 and x = 2 k π ∓ ln 2 ± 3 . Fortunately, of the options provided, the part outside the logarithm has magnitude less than 2 π , so we can drop all the 2 k π to get x = ± ln 2 ± 3 or x = ∓ ln 2 ± 3 . Now, I used the complimentary angle identity: sin x = cos 2 π − x , letting sin x = 2 : 2 π − x = ± ∓ ln 2 ± 3 , so we have x = 2 π ± ∓ ln 2 ± 3 . Check the options and only one match this form.
Are the options 2 π ± i ( ln ( 2 + 3 ) ) and 2 π ± i ( ln ( 2 − 3 ) ) identical?
Yes they are same.
Why have we not considered the cases in which there is 3 π / 2 instead of π / 2 . If we do then we get four solutions to the given question. Do you have any idea about this?
Log in to reply
I don't think that replacing π / 2 by 3 π / 2 are still solutions. Can you elaborate more on it?
Log in to reply
Check the link which I have provided in my answer to get an idea of what I am saying.
The answer gets very complicated difficult for me to type in. A direct link to a website is given which provides the direct formula and its proof for these sin problems.