Cra𝓏-𝑒 coπplex
If y is the crazy function in terms of x that satisfies the equation:
( e 2 π y 3 x 1 − y 2 ) i − ( e 2 π x 1 − y 2 y 3 ) i = 2 y
Then compute:
∫ − ∞ 0 1 + y ( x ) d x + ∫ 0 ∞ 1 − y ( x ) d x
The answer can be written in the form b a e a π + a e − a π , where a and b are coprime integers. Enter ∣ a ∣ + ∣ b ∣ .
Notes: i = − 1
Assume the positive branch of the square root is used.
Hint : If you end up using any inverse or trigonometric functions, use the main branch, for example: arcsin r = θ + 2 k π with k = 0
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
@Saúl Huerta That was a fun problem! Even though I did the same as you to solve it, I'm still not sure about some details where you "invert" the functional equation: y = sin ( ln y 6 x 2 ( 1 − y 2 ) ) = : f ( x , y ) , f ( − x , y ) = f ( x , y ) , ∣ y ∣ = ∣ f ( x , y ) ∣ ≤ 1
- Shouldn't y ( x ) be mirror-symmetric to the y-axis? If ( x , y ) is a solution, so is ( − x , y ) after all (closely related to 3.)
-
The functional equation has multiple solutions: y = f ( x , y ) ⇒ ln y 6 x 2 ( 1 − y 2 ) = arcsin ( y ) + 2 k π ∨ ln y 6 x 2 ( 1 − y 2 ) = − arcsin ( y ) + ( 2 k + 1 ) π ∣ ∣ ∣ k ∈ Z These additional constants become factors when we solve for x and thereby change the value of the integral later
-
What happened to the absolute values when we simplify the radical? Shouldn't the fundamental solution for k = 0 be ∣ x ∣ = 1 − y 2 ∣ y ∣ 3 e arcsin ( y ) As far as I can tell, the functional equation remains valid for arbitrary choices of signs for x , so one should be able to construct a discontinuous function y ( x ) that satisfies the functional equation. Of course such a function might not be invertible anymore, e.g. g : ( − 1 ; 1 ) → R , g ( y ) : = 1 − y 2 y 3 e arcsin ( y ) invertible , y ( x ) : = { g − 1 ( − x ) : g − 1 ( x ) : x ∈ ( − 1 ; 1 ) ∩ Q else As far as I can tell, y ( x ) satisfies the functional equation, is discontinuous (almost) everywhere and is not invertible. The integrals would not converge for this choice of y ( x ) , because it has too many discontinuities.
Suggestion: Define y as a continuous function with s g n ( x ) = s g n ( y ) (or something similar) to get rid of the problems with absolute values. Not sure what to do about the set of solutions k ∈ Z ...
Log in to reply
@Carsten Meyer Hey thanks for your very detailed reply! Sorry if the problem was vague but I tend to forget some important technical nuances which is what happened here. With respect to the absolute value, I will simplify the radical within the functional equation so that there are no discontinuities (which is why I originally intended but when writing the problem in the latex editor I decided to put the whole fraction in the radical for aesthetic purposes, but now that I think about it it was stupid lol): ( e 2 π y 3 x 1 − y 2 ) i − ( e 2 π x 1 − y 2 y 3 ) i = 2 y
And about the cyclic properties of the trigonometric function within the problem I will specify to use the main branch k = 0 . Thanks for helping me remember the theory and maintain mathematical consistency! I sometimes forget it lol, will edit the problem asap :D. (Edit: I edited the problem I think now it should be fine, if there is still something wrong I would be very glad if you let me know. In the future maybe I will even leave the multiple solutions for k ∈ Z including the branch with the negative inverse sine, but for now I will leave the specifications as they are while I work in the more general solution. The absolute value problems do have to go though to ensure continuity and to allow for an inverse function).
Log in to reply
@Saúl Huerta You're welcome! I know I'm sort of nitpicky about these details - it's the way some people learn ;) Mentioning the fundamental branch of square-root and the inverse trig functions should do the trick!
The first step is to transform the equation into something more manageable to check if there even exists an expression for y in terms of known functions. We can see that the e π can be factored out of both terms to get the constant e − i 2 π , which is equal to − i , which is equal to i 1 . We can divide both sides by 2 and use the identity 2 i e i θ − e − i θ = sin θ to rewrite as follows: y = 2 i ( y 6 x 2 ( 1 − y 2 ) ) i − ( y 6 x 2 ( 1 − y 2 ) ) − i = sin ( ln y 6 x 2 ( 1 − y 2 ) ) ⟹ e arcsin y = y 3 x 1 − y 2 It is clear that y ( x ) ∈ ( − 1 , 1 ) and the function is continuous for x ∈ R . Now, finding an expression for y seems to be very difficult, if not impossible. Instead let's take a look at the graph of its inverse function y − 1 ( x ) = 1 − x 2 x 3 e arcsin x :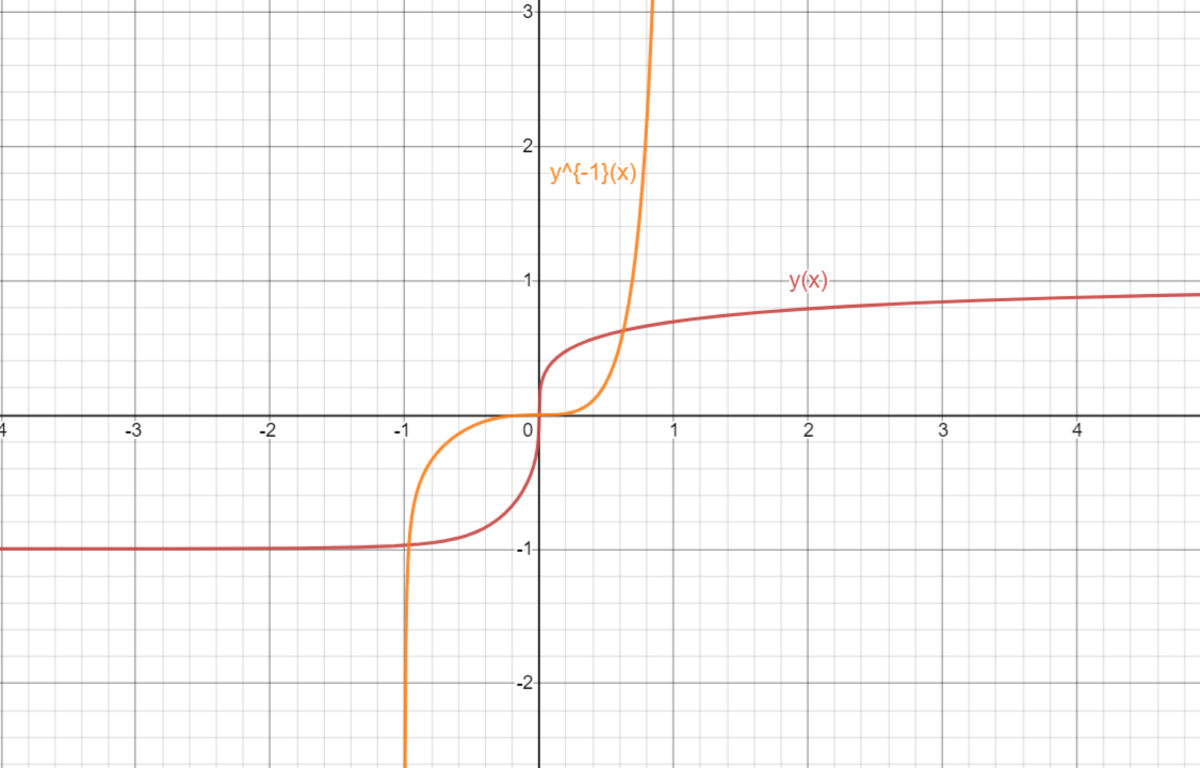 Since the inverse function is obtained by reflecting the function with respect to the
x
-axis and then rotating the original function 90 degrees the integral we are trying to compute becomes:
∫
−
1
1
1
−
x
2
x
3
e
arcsin
x
d
x
In its current form, this integral is screaming for a trig sub, so we substitute
x
=
sin
θ
:
=
∫
−
2
π
2
π
e
θ
sin
3
θ
d
θ
Here we could do some integration by parts but I find it much better if we do some neat substitutions to greatly simplify the calculations. We know that
sin
3
θ
=
4
3
sin
θ
−
sin
3
θ
and
sin
θ
=
2
i
e
i
θ
−
e
−
i
θ
. After substituting these identities in succession respectively and simplifying we end up with four very simple, neat and easy exponential integrals:
=
8
i
3
∫
−
2
π
2
π
e
(
1
+
i
)
θ
d
θ
−
8
i
3
∫
−
2
π
2
π
e
(
1
−
i
)
θ
d
θ
−
8
i
1
∫
−
2
π
2
π
e
(
1
+
3
i
)
θ
d
θ
+
8
i
1
∫
−
2
π
2
π
e
(
1
−
3
i
)
θ
d
θ
Integrating and doing all the algebra yields:
∫
−
1
1
1
−
x
2
x
3
e
arcsin
x
d
x
=
5
2
e
2
π
+
2
e
−
2
π
Therefore
a
+
b
=
2
+
5
=
7
Since the inverse function is obtained by reflecting the function with respect to the
x
-axis and then rotating the original function 90 degrees the integral we are trying to compute becomes:
∫
−
1
1
1
−
x
2
x
3
e
arcsin
x
d
x
In its current form, this integral is screaming for a trig sub, so we substitute
x
=
sin
θ
:
=
∫
−
2
π
2
π
e
θ
sin
3
θ
d
θ
Here we could do some integration by parts but I find it much better if we do some neat substitutions to greatly simplify the calculations. We know that
sin
3
θ
=
4
3
sin
θ
−
sin
3
θ
and
sin
θ
=
2
i
e
i
θ
−
e
−
i
θ
. After substituting these identities in succession respectively and simplifying we end up with four very simple, neat and easy exponential integrals:
=
8
i
3
∫
−
2
π
2
π
e
(
1
+
i
)
θ
d
θ
−
8
i
3
∫
−
2
π
2
π
e
(
1
−
i
)
θ
d
θ
−
8
i
1
∫
−
2
π
2
π
e
(
1
+
3
i
)
θ
d
θ
+
8
i
1
∫
−
2
π
2
π
e
(
1
−
3
i
)
θ
d
θ
Integrating and doing all the algebra yields:
∫
−
1
1
1
−
x
2
x
3
e
arcsin
x
d
x
=
5
2
e
2
π
+
2
e
−
2
π
Therefore
a
+
b
=
2
+
5
=
7