Complexity! (3)
If is a complex number of unit modulus whose argument is , find .
Notations:
- denotes the conjugate of .
- denotes the argument of a complex number.
For more problems on complex numbers, click here .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.

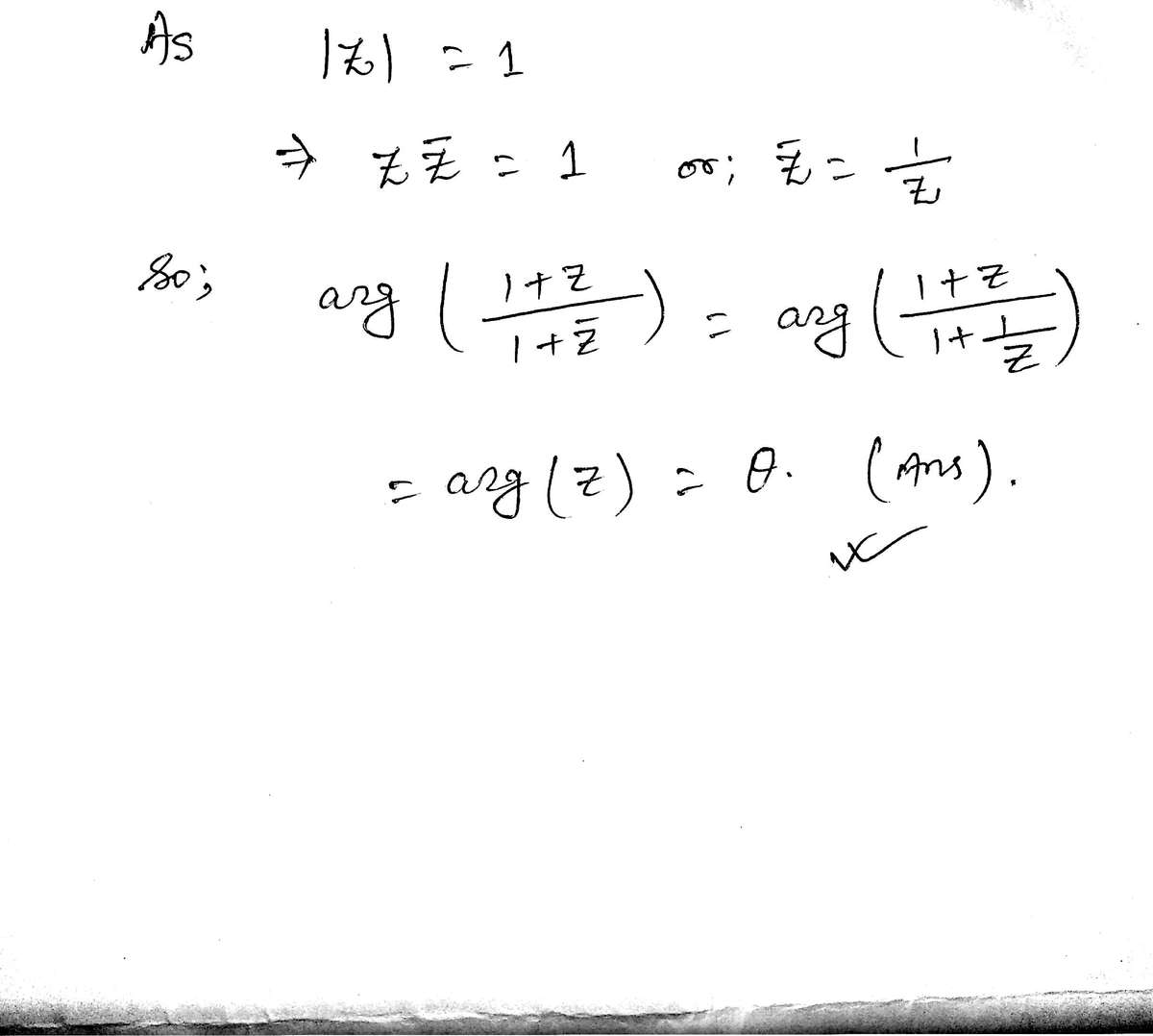
It is given that z = ∣ z ∣ e i θ = e i θ ⟹ z ˉ = e − i θ . Then we have:
1 + z ˉ 1 + z = 1 + e − i θ 1 + e i θ = 1 + cos θ − i sin θ 1 + cos θ + i sin θ = 1 + 1 + t 2 1 − t 2 − i 1 + t 2 2 t 1 + 1 + t 2 1 − t 2 + i 1 + t 2 2 t = 2 − i 2 t 2 + i 2 t = 1 − i t 1 + i t = 1 − i t 1 + i t ⋅ 1 + i t 1 + i t = 1 + t 2 1 − t 2 + i 2 t = cos θ + i sin θ = e i θ = z By Euler’s formula, Let t = tan 2 θ , cos θ = 1 + t 2 1 − t 2 , sin θ = 1 + t 2 2 t
Therefore, we have:
ar g ( 1 + z ˉ 1 + z ) = ar g ( z ) = θ