Complex+real?

Algebra Level 5

( 1 + 2 i ) x 3 − 2 ( 3 + i ) x 2 + ( 5 − 4 i ) x + 2 a 2 = 0 (1+2i)x^{3}-2(3+i)x^{2}+(5-4i)x+2a^{2}=0

Let a a be a real number, and the equation above have at least one real root (of x x ).

What is the value of ∑ a 2 \sum a^{2} ?

Details and Assumptions :

  • i 2 = − 1 i^{2}=-1 .

  • ∑ a 2 \sum a^{2} represents sum of squares of all possible values of a a .


The answer is 18.

View wiki
Tanishq Varshney by Tanishq Varshney , 23, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Vagish Jha
May 13, 2015

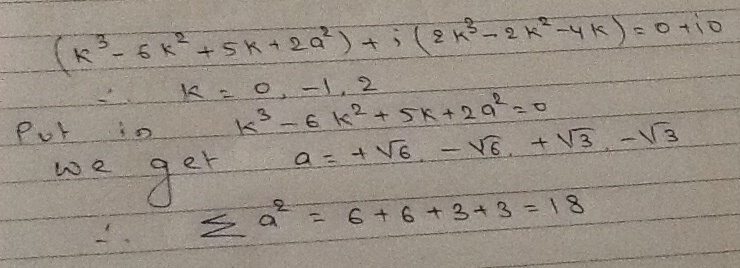Mostly seen questions posted put x=k and equate real and imaginary part zeo. We get four different value of a

6 Helpful 0 Interesting 0 Brilliant 0 Confused

i mistook as sum of all possible values of a^2(which is 9)

NILAY PANDE - 6 years ago
Aakash Khandelwal
May 14, 2015

we may rewrite the given equation as:

(x^3- 6x^2+ 5x+2a^2 )+2i(x^3-x^2-2x)=0

which is of the form c+id=0

hence c=0 and d=0

for d=0 : x= {-1,0,2}

for these x, a^2={0 , (6^0.5 ), (-6^0.5) , (3^0.5) , (-3^0.5)}

hence summation a^2= 9*2=18.

1 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...