Complicated Tangency of a system of Circles!
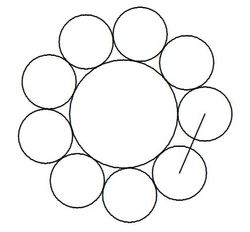 Nine circles of radius
2
1
are externally tangent to a circle of radius
1
and also are tangent to one another as shown. If the distance between the centers of the first and the last of the circles can be expressed as:
Nine circles of radius
2
1
are externally tangent to a circle of radius
1
and also are tangent to one another as shown. If the distance between the centers of the first and the last of the circles can be expressed as:
C A B
where A , B , C are positive integers satisfying g cd ( A , C ) = 1 and B is squarefree, find the value of A + B + C .
Here is a junior version of this problem - Twisting the Problem - "Complicated Tangency of a system of circles
The answer is 4093.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
You don't need to find the exact polynomial of cos ( 8 θ ) . You just need to do this:
cos θ = 9 7
⇒ cos ( 2 θ ) = 2 cos 2 ( θ ) − 1
⇒ cos ( 4 θ ) = 2 cos 2 ( 2 θ ) − 1
⇒ cos ( 8 θ ) = 2 cos 2 ( 4 θ ) − 1 .
Log in to reply
Finding out cos(8 theta) was going tedious so I opted for discuss solutions
It's practically the same thing, isn't it?
Log in to reply
Yes. But you substitute the value of cos ( θ ) at the end whereas I substitute it from the very start thus saving the work. It's tedious, but less work.
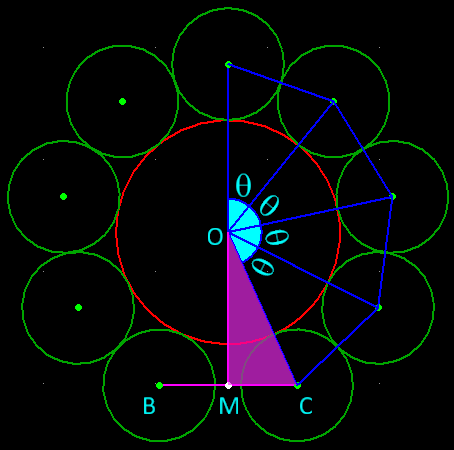 The desired distance BC can be found using the triangle
Δ
O
M
C
,
O
C
=
2
3
, and
M
C
=
O
C
sin
4
θ
cos
θ
=
2
(
2
3
)
(
2
3
)
(
2
3
)
2
+
(
2
3
)
2
−
1
2
=
9
7
;
sin
θ
=
9
4
2
sin
2
θ
=
2
sin
θ
cos
θ
=
8
1
5
6
2
;
cos
2
θ
=
8
1
1
7
sin
4
θ
=
2
sin
2
θ
cos
2
θ
=
8
1
2
1
9
0
4
2
B
C
=
2
M
C
=
2
(
2
3
)
sin
4
θ
=
2
1
8
7
1
9
0
2
2
The desired distance BC can be found using the triangle
Δ
O
M
C
,
O
C
=
2
3
, and
M
C
=
O
C
sin
4
θ
cos
θ
=
2
(
2
3
)
(
2
3
)
(
2
3
)
2
+
(
2
3
)
2
−
1
2
=
9
7
;
sin
θ
=
9
4
2
sin
2
θ
=
2
sin
θ
cos
θ
=
8
1
5
6
2
;
cos
2
θ
=
8
1
1
7
sin
4
θ
=
2
sin
2
θ
cos
2
θ
=
8
1
2
1
9
0
4
2
B
C
=
2
M
C
=
2
(
2
3
)
sin
4
θ
=
2
1
8
7
1
9
0
2
2
This is rather a tedious solution, hope to find some nicer one: Joining the centres of each of the small circles with the centre of the big circle we form 9 angles around the centre of the big circle. 8 of these angles are equal to, say, θ , and the one inside the triangle made by the distance wanted ( d ) should be 3 6 0 ˚ − 8 θ . Since all θ 's are inside triangles of sides 3/2, 3/2 and 1, we can use the cosine theorem to find θ to satisfy
1 2 = ( 2 3 ) 2 + ( 2 3 ) 2 − 2 ( 2 3 ) ( 2 3 ) cos θ ⟹ cos θ = 9 7
Since the remaining angle is inside a triangle of sides 3/2, 3/2 and ( d ), we can use the cosine theorem again to write
d 2 = ( 2 3 ) 2 + ( 2 3 ) 2 − 2 ( 2 3 ) ( 2 3 ) cos ( 3 6 0 ˚ − 8 θ ) ⟹ d 2 = 2 9 ( 1 − cos 8 θ )
Now, applying the double-angle formula for cosine three times we get
cos 8 θ = 1 2 8 cos 8 ( θ ) − 2 5 6 cos 6 ( θ ) + 1 6 0 cos 4 ( θ ) − 3 2 cos 2 ( θ ) + 1 .
Substituting this and simplifying, we get
d = 2 1 8 7 1 9 0 4 2