Composite 3D solid - Special Ratio of Edge Lengths

Geometry Level 4

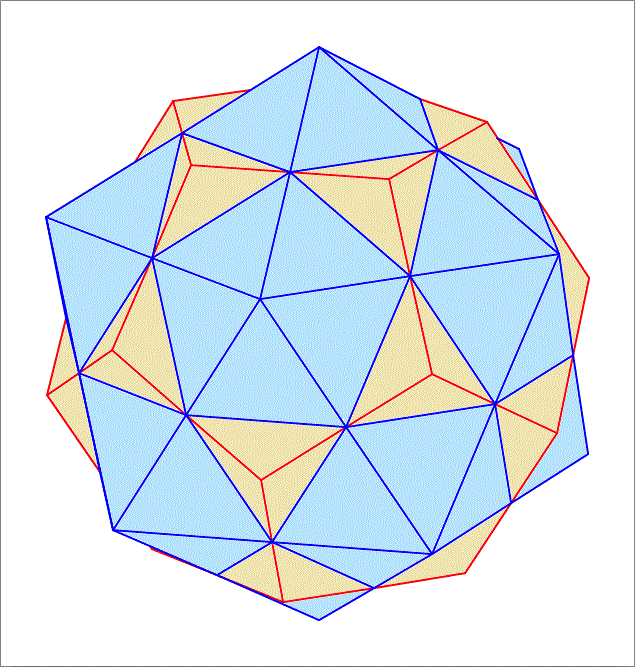
A regular dodecahedron (shown in the figure above with red edges), and a regular icosahedron (blue edges) share the same center and are oriented in such a way that the vertices of the icosahedron all lie on the normals to the faces of the dodecahedron drawn from the centers of the faces, as the figure above illustrates. Further, the edges of the icosahedron intersect the edges of the dodecahedron. Using this fact, and the information below about the inradius and circumradius of both the unit regular dodecahedron and the unit regular icosahedron, find the ratio of the edge length of the icosahedron to the edge length of the dodecahedron.

Details and Assumptions:

The inradius and circumradius of a unit regular dodecahedron are given by, respectively, $r_D = \dfrac{1}{20} \sqrt{250 + 110 \sqrt{5}}$ and $R_D = \dfrac{1}{4} (\sqrt{15} + \sqrt{3})$
The inradius and circumradius of a unit regular icosahedron are given by, respectively, $r_I = \dfrac{1}{12} (3 \sqrt{3} + \sqrt{15})$ and $R_I = \dfrac{1}{ 4} \sqrt{10 + 2 \sqrt{5}}$

\dfrac{1 +\sqrt{5} }{2}

\dfrac{5 +\sqrt{5} }{4}

\dfrac{2 +\sqrt{2} }{2}

\dfrac{-1 +\sqrt{5} }{2}

2 solutions

Michael Mendrin
Oct 20, 2018

The three triangular faces of the pyramid with an equilateral triangle base have an apex angle of $108°$ . Hence, the ratio of the edges of the icoscahedron and of the dodecahedron is

$2Sin(54) = \frac{1}{2}(1+\sqrt{5})$

Otto Bretscher
Oct 20, 2018

Using the given circumradii, we find the midradii to be $\frac{1}{4}(3+\sqrt{5})D$ and $\frac{1}{4}(1+\sqrt{5})I$ , where $D$ and $I$ the edge lengths. These have to be equal since the edges intersect in the middle, so that $\frac{I}{D}=\frac{1}{2}(1+\sqrt{5})$ .

Composite 3D solid - Special Ratio of Edge Lengths

2 solutions

0 pending reports