Composite area
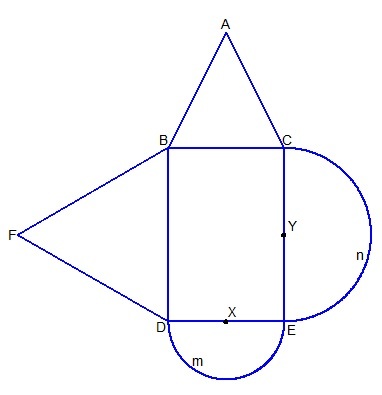 The diameter of semicircle
with center at
is thrice the radius of semicircle
with center at
. Quadrilateral
is a rectangle and triangle
is an equilateral triangle. The altitude of triangle
is twice the radius of semicircle
. If the area of triangle
is
, find the area of the whole figure.
The diameter of semicircle
with center at
is thrice the radius of semicircle
with center at
. Quadrilateral
is a rectangle and triangle
is an equilateral triangle. The altitude of triangle
is twice the radius of semicircle
. If the area of triangle
is
, find the area of the whole figure.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
A A B C = 2 1 b h
3 2 = 2 1 ( 2 r ) ( 2 r )
6 4 = 4 r 2
1 6 = 4 r
r = 4
It follows that the diameter of semicircle n is 3 ( 4 ) = 1 2 and C E = B D = 1 2 and D E = B C = 8 .
So the area of semicircle n is 2 1 π ( 4 2 ) = 8 π . The area of semicircle m is 2 1 π ( 6 2 ) = 1 8 π . The area of rectangle B C E D is 8 ( 1 2 ) = 9 6 . The area of equilateral triangle F B D is 4 3 ( 1 2 2 ) = 3 6 3 .
Finally, the area of the whole figure is
3 2 + 9 6 + 3 6 3 + 8 π + 1 8 π = 1 2 8 + 3 6 3 + 2 6 π
Formulas used:
A = π r 2 ⟹ Area of a circle where r is the radius. When looking for the area of a semicircle, we need to divide it by 2 .
A = 4 3 x 2 ⟹ Area of an equilateral triangle where x is the side length. It is a derived formula.
A = l w ⟹ Area of a rectangle where l is the length and w is the width. It can also be b a s e × h e i g h t or l e n g t h × b r e a d t h