composite figures area problem
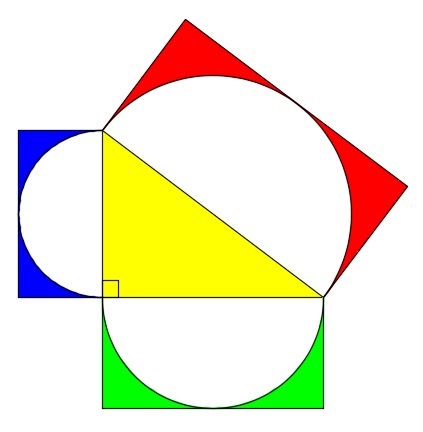 In the figure above, all arcs are semi-circles. The area of the red region is
. The area of the blue region is
. The area of the green region is
. What is the area of the yellow right triangle?
In the figure above, all arcs are semi-circles. The area of the red region is
. The area of the blue region is
. The area of the green region is
. What is the area of the yellow right triangle?
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Consider a region like the ones painted red, blue or green in the given diagram. Its area is the difference between the area of a rectangle and a semi-circle, and if the radius of the semicircle is r , then the rectangle has dimensions 2 r × r . Thus the area such a region can be written as
2 r 2 − 2 1 π r 2 = 2 r 2 ( 4 − π )
Re-writing the given areas in this form, we get
A R E D A B L U E A G R E E N = 1 2 . 5 − 3 . 1 2 5 π = 4 . 5 − 1 . 1 2 5 π = 8 − 2 π = 3 . 1 2 5 ( 4 − π ) = 1 . 1 2 5 ( 4 − π ) = 2 ( 4 − π ) ⟹ ⟹ ⟹ r R = 2 . 5 r B = 1 . 5 r G = 2
Thus the yellow triangle is 3 - 4 - 5 and its area is 2 1 ( 3 ) ( 4 ) = 6