composite function by many "layers"
Algebra
Level
pending
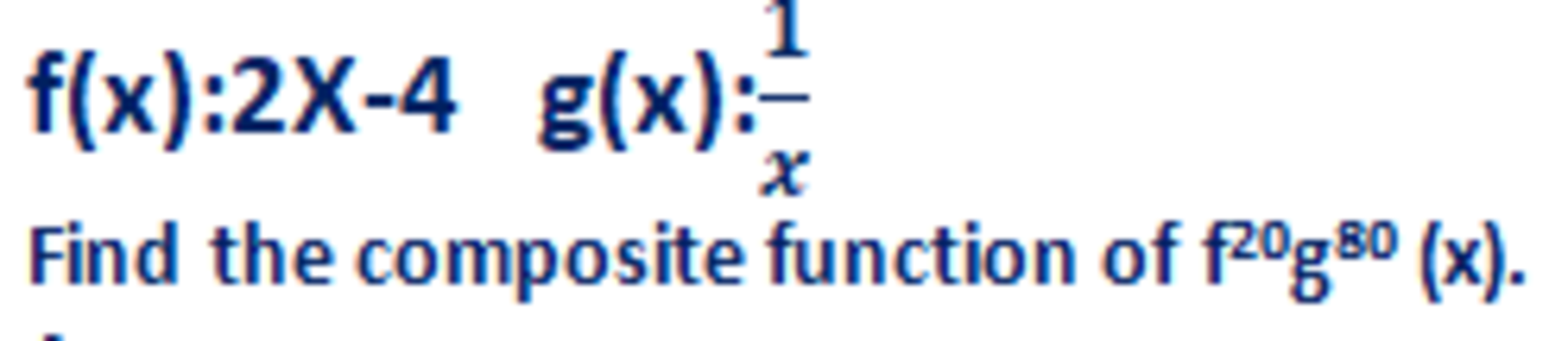 answer can expressed as c(ax-b), where ax-b is factor by c [e.g. (4x-8) factorise to 4(x-2)] and c is positive integer. Find the value of c.
answer can expressed as c(ax-b), where ax-b is factor by c [e.g. (4x-8) factorise to 4(x-2)] and c is positive integer. Find the value of c.
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
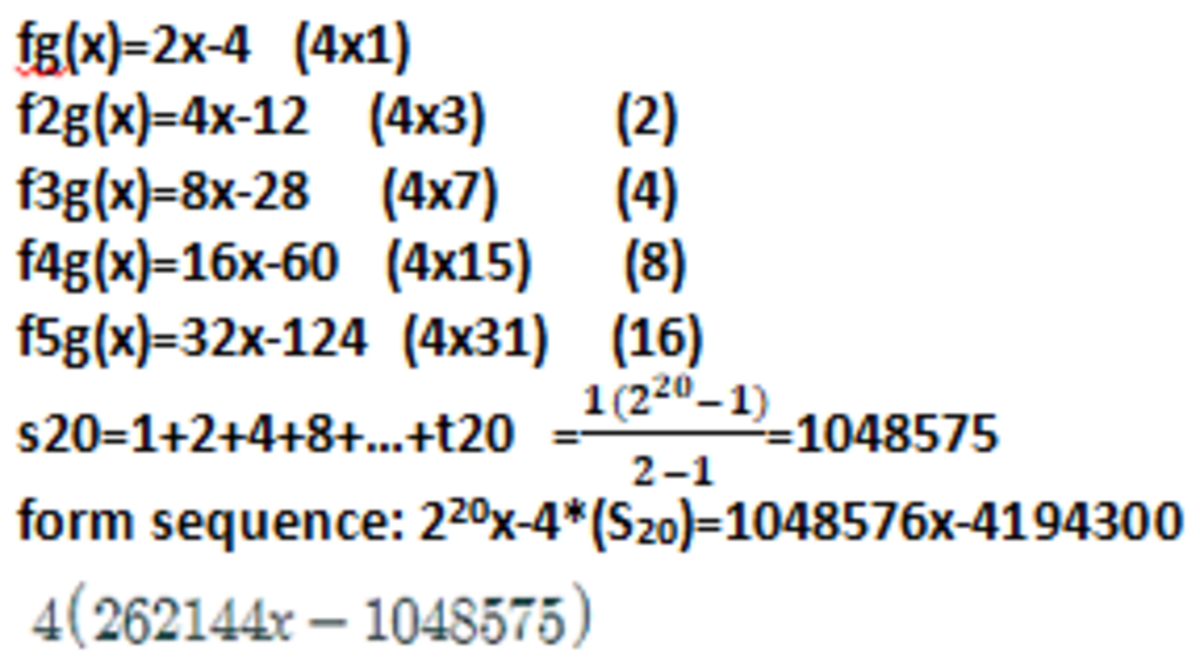
Since g g is the identity map, g 8 0 is the identity map, so we just need to calculate f 2 0 . Now f ( x ) − 4 = 2 ( f − x ) , so f n ( x ) − 4 = 2 n ( x − 4 ) (by induction), and so f n ( x ) = 4 [ 2 n − 2 x − ( 2 n − 1 ) ] Thus a = 2 n − 2 , b = 2 n − 1 and c = 4 for any n ≥ 2 . Since b is odd, a and b are coprime.