Composite Load Voltage
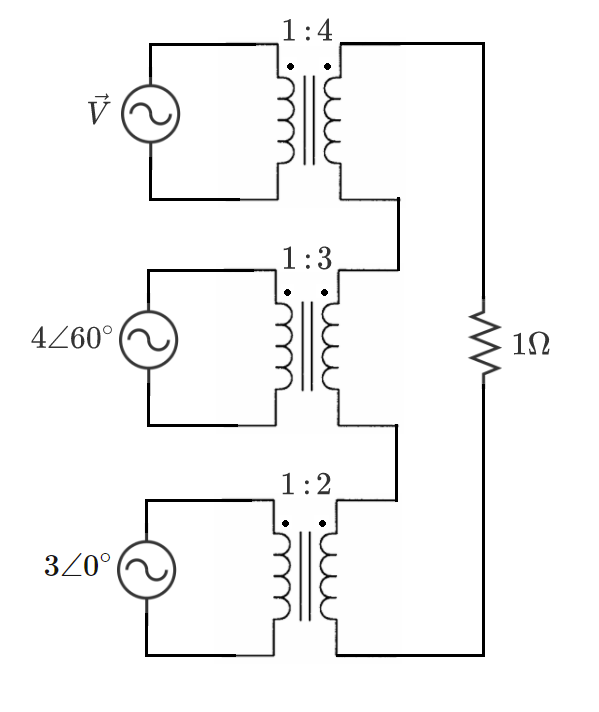
Three ideal AC voltage sources feed the primary windings of three ideal transformers, and the transformer secondary windings are connected together to serve a resistive load.
RMS source voltages, transformer winding ratios, winding connections, and load resistance are shown in the diagram.
What is the minimum possible RMS magnitude of such that the load resistor dissipates of power?
The answer is 1.4686.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The load voltage is the sum of the scaled input voltages. As long as the magnitude of the load voltage is 10, it doesn't matter what the angle is.
2 × 3 ∠ 0 ∘ + 3 × 4 ∠ 6 0 ∘ + 4 × V = 1 0 ∠ θ
Consolidate the known terms:
1 5 . 8 7 4 5 ∠ 4 0 . 8 9 3 4 ∘ + 4 × V = 1 0 ∠ θ
We can get the smallest V if we choose a load voltage angle equal to 40.8934 degrees.
1 5 . 8 7 4 5 ∠ 4 0 . 8 9 3 4 ∘ + 4 × V = 1 0 ∠ 4 0 . 8 9 3 4 ∘ ⟹ V = 1 . 4 6 8 6 ∠ − 1 3 9 . 1 0 6 6 ∘