Compressing A Single-Particle Gas
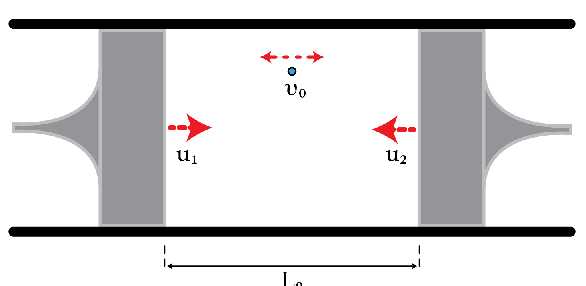
Consider a particle moving between two pistons as shown in the figure. The distance between the pistons is reduced slowly (as slowly as you want), i.e., and the collisions are perfectly elastic. In this problem, we want to determine the equation of state relating the speed of the particle and the distance between the pistons . Initially, the speed of the particle is and the distance between the pistons is . Find the speed of the particle in meters per second when the distance between the pistons becomes
The answer is 900.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the particle hit a wall n times per second, then, the force applied is clearly 2 m v n .
Also time taken to come back and strike again = T = v 2 l
Hence, n = T 1 = 2 L v
Hence, force applied on a wall is given by : L m v 2 .
Now, in order to move the piston slowly, F e x t is also L m v 2 . Clearly, the work done by this force would add into its kinetic energy. Note that this force is acting at two ends. Say left piston moves d l 1 and right piston moves d l 2 , then
− L m v 2 ( d l 1 + d l 2 ) = − L m v 2 d L = d ( 2 m v 2 ) , where d ( 2 m v 2 ) = m v d v
Hence, − L d L = v d v
Or − ∫ L 0 3 L 0 L d L = ∫ v 0 v ′ v d v , ⇒ v ′ = 3 v 0 = 9 0 0 m / s