Compute $\sqrt{5}$ using Bisection method

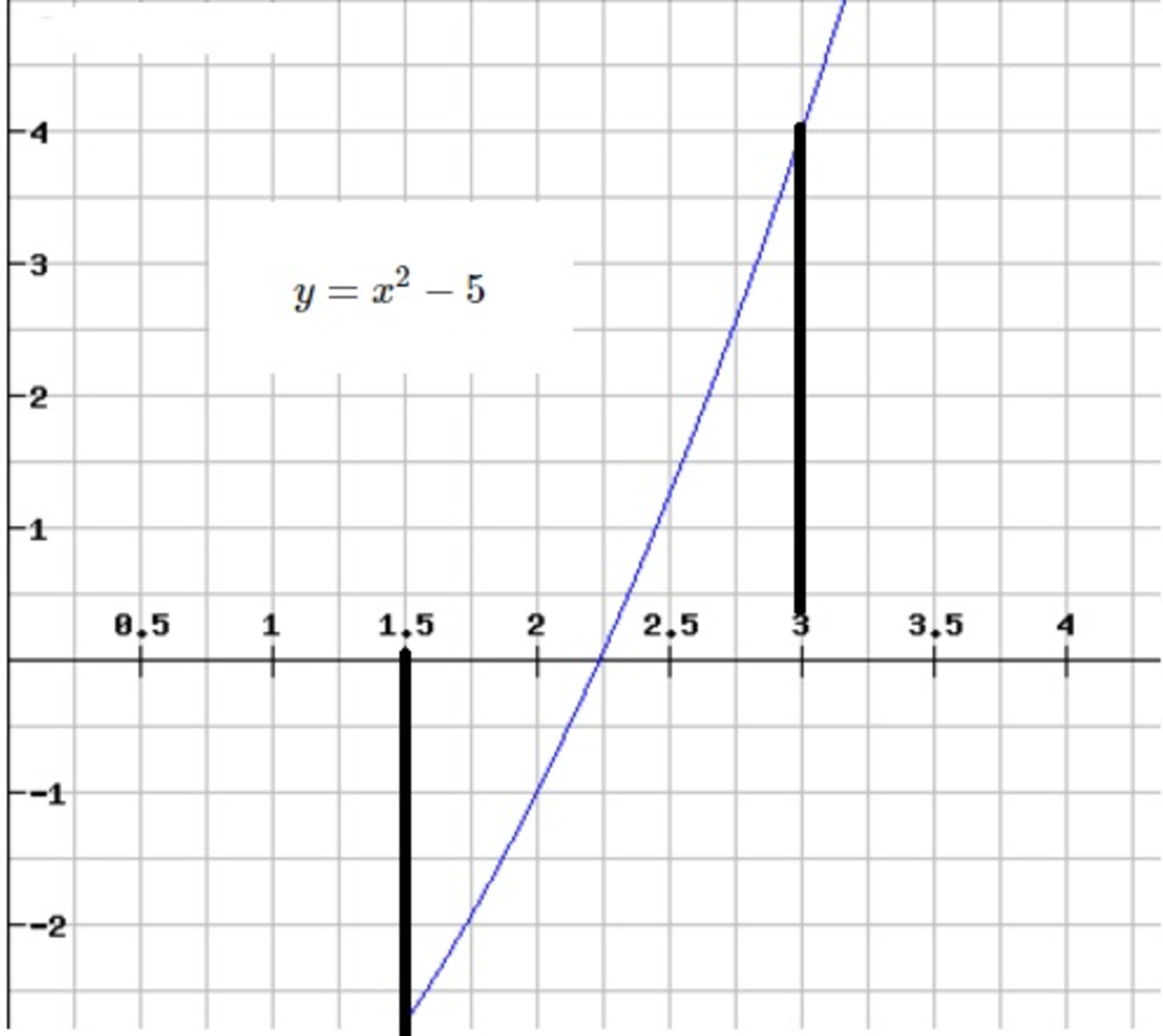
With the help of the bisection method, let us try to find $\sqrt{5}$ by using the following equation $y(x) = x^2 -5$ Bisection is a Binary search method which is based on the Intermediate Value Theorem. Using bisection method to find $\sqrt{5}$ , we start by a closed interval $[a,b]$ on which $\large y$ changes sign, We divide the interval in half. We then replace $[a,b]$ by the half-interval on which
$\large y$ changes sign. This process is repeated until the interval has a total length less than certain tolerance $\large \epsilon$ .

If we started with an interval $ab$ of length $1.5$ , where $a = (1.5,0)$ and $b = (3,0)$ . [note that $y(a) = - 3,75 < 0,$ and $y(b) = 4 > 0$ ].
Find the number of steps required to find $\sqrt{5}$ when $\large \epsilon = 10^{-6}$ ?