It escalates very quickly!

Computer Science Level 2

A ( m , n ) = { n + 1 if m = 0 A ( m − 1 , 1 ) if m > 0 and n = 0 A ( m − 1 , A ( m , n − 1 ) ) if m > 0 and n > 0 A(m,n) = \begin{cases}\begin{array} { l l } n + 1 & \text{ if } m=0 \\ A(m-1,1) & \text{ if } m>0 \text{ and } n=0 \\ A\big(m-1, A(m,n-1)\big) & \text{ if } m>0 \text{ and } n>0 \end{array} \end{cases}

Consider the Ackermann function as described above.

Find A ( 3 , 3 ) A(3 ,3 ) .


The answer is 61.

Vlad Vasilescu by Vlad Vasilescu , 22, Romania

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

Vlad Vasilescu
Dec 29, 2016

A simple C++ code :

4 Helpful 0 Interesting 0 Brilliant 0 Confused

Anyone trying to solve this by hand: the Ackermann fucntion itself is called 2432 times, so just don't.

Kai Ott - 4 years, 5 months ago
Sharky Kesa
Jan 2, 2017 
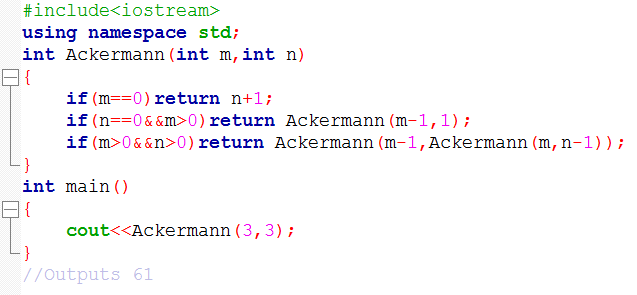
1
2
3
4
5
6
7
8
9
 
def A(m,n):
    if m==0:
        return n+1
    elif m>0 and n==0:
        return A(m-1,1)
    elif m>0 and n>0:
        return A(m-1,A(m,n-1))

print(A(3,3))

This outputs 61 as your answer.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

Contrary to what @Kai Ott recommends, I actually did the problem by hand. After 45 minutes of writing 65 Ackermann functions, I noticed certain patterns that allowed me to finish the problem in other 15 minutes, having written only 105 out of the 2432 Ackermann functions.

Document of my resolution https://drive.google.com/file/d/0B6ZL97ZT42IhQzVDZFJuZlhsMG8/view?usp=sharing

0 Helpful 0 Interesting 0 Brilliant 0 Confused

I'm curious. Why waste so much time ?

Vlad Vasilescu - 4 years, 5 months ago

Didn't actually think it would take that long. Plus, it was really entertaining and challenging, and I like being challenged.

Diego Emmanuel Lee Rodriguez - 4 years, 5 months ago

Log in to reply

That's what I did. I started off by finding the pattern for A(1,x) which always gives x+2 and then I found it for A(2,x) which always gives 2x+3. With these things in mind, you can solve in 9 lines.

  1. A(3,3)
  2. A(2,A(3,2))
  3. A(2,A(2,A(3,1)))
  4. A(2,A(2,A(2,A(3,0))))
  5. A(2,A(2,A(2,A(2,1))))
  6. A(2,A(2,A(2,5)))
  7. A(2,A(2,13))
  8. A(2,29)
  9. 61

Adam Hufstetler - 4 years, 5 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...