Concentric circles and equilateral triangle
Three concentric circles each have radii 8 cm , 1 5 cm , 1 7 cm .
If the largest possible area of the equilateral triangle with one vertex on each circle is of the form
(
a
+
b
4
3
)
cm
2
,
where
a
and
b
are positive integers, find
a
+
b
.
The answer is 379.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
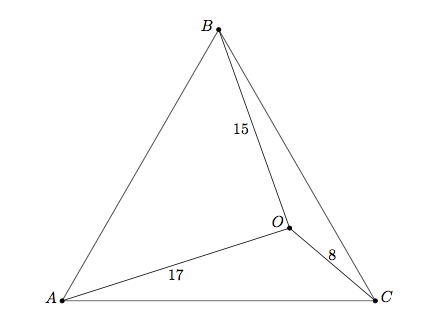
Notice that the side length of this largest equilateral triangle is equal to the side length of equilateral triangle A B C shown below
where O is the centre of the concentric circles. Now rotate the triangle 6 0 ∘ anticlockwise about A to form the points B ′ and O ′ .
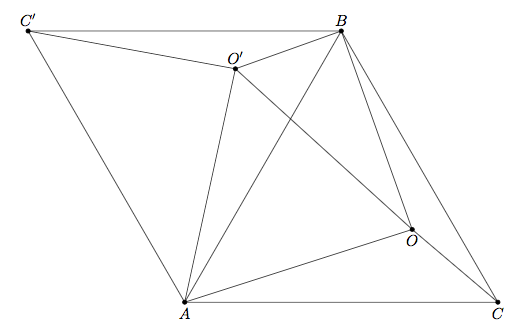
Since it is evident that ∠ O ′ A O = 6 0 ∘ and A O ′ = A O = 1 7 , we deduce that △ A O ′ O is equilateral, and thus O ′ O = 1 7 . Notice that 8 2 + 1 5 2 = 1 7 2 , so we can now apply the converse of Pythagoras's Theorem to △ O ′ B O to deduce that ∠ O ′ B O = 9 0 ∘ . Then ∠ A O ′ B + ∠ A O B = 3 6 0 − 6 0 − 9 0 = 2 1 0 ∘ , meaning that ∠ B O C = 3 6 0 − 2 1 0 = 1 5 0 ∘ .
So we can apply the Cosine rule to △ B O C to obtain B C = 8 2 + 1 5 2 − 2 × 8 × 1 5 × cos ( 1 5 0 ) = 1 2 0 3 + 2 8 9 and thus the area of the triangle is ( 1 2 0 3 + 2 8 9 ) × 4 3 = 9 0 + 4 2 8 9 3 cm 2 So the answer is 9 0 + 2 8 9 = 3 7 9 .
Nice argument, but you miss the other solution by assuming that O lies inside the triangle...
Log in to reply
Good point. Looking at your diagram made it seem obvious which triangle was the larger - I was really just trying to attack the problem of finding the area once it is known which triangle is larger; a similar method could be used to determine the area of the smaller triangle if you wanted to write a complete solution.
I don't see the point why [\angle BOC=360\degree-210\degree= 150\degree]
Log in to reply
Remember that ∠ A O C = ∠ A O ′ B . since one is obtained from the other by rotation.
Let A , B , C be the vertices of the triangle on the circles of radii 8 , 1 5 , 1 7 respectively. Since we can reflect the triangle if necessary, we can assume that A , B , C occur on the triangle in anticlockwise order. We can then assume that A is represented by the complex number 8 and that B is represented by the complex number 1 5 e i θ for some − π < θ ≤ π . As the third vertex of an equilateral triangle, occurring in anticlockwise order, C will then be represented by the complex number 8 − ω 2 ( 1 5 e i θ − 8 ) = − 8 ω − 1 5 ω 2 e i θ = − ω ( 8 + 1 5 ω e i θ ) Since C must lie on the circle of radius 1 7 , we deduce that ∣ 8 + 1 5 ω e i θ ∣ = 1 7 , which implies that cos ( θ + 3 2 π ) = 0 . Thus we deduce that θ = 6 5 π , − 6 1 π .
The side of the equilateral triangle is h , where h 2 = ∣ 1 5 e i θ − 8 ∣ 2 = 2 8 9 − 2 4 0 cos θ = 2 8 9 ± 1 2 0 3 , and hence the area of the triangle is A = 4 1 h 2 3 = 4 1 3 ( 2 8 9 ± 1 2 0 3 ) = 4 2 8 9 3 ± 9 0 Thus there are two types of equilateral triangle possible, and the area of the larger one is 9 0 + 4 2 8 9 3 , making the answer 9 0 + 2 8 9 = 3 7 9 .