Conceptual Physics: II
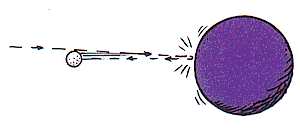 You have a friend who says that: "After a golf ball collides with a bowling ball at rest, although the speed gained by the bowling ball is very small, its momentum exceeds the initial momentum of the golf ball." Your friend further asserts that this is related to the "negative" momentum of the golf ball after collision.
You have a friend who says that: "After a golf ball collides with a bowling ball at rest, although the speed gained by the bowling ball is very small, its momentum exceeds the initial momentum of the golf ball." Your friend further asserts that this is related to the "negative" momentum of the golf ball after collision.
Your another friend says this is hogwash, and thinks that the momentum conservation would be violated. Which friend do you agree with, and why?
A. The first friend:
We have The bowling ball's momentum exceeds that of the initial momentum of the golf ball, but this is to account for the "negative" momentum of the golf ball. The opposite momenta cancel, and the Law of Conservation of Momentum is not violated.
B. The second friend:
By the Law of Conservation of Momentum , . Since the momentum of the bowling ball was initially zero, the momentum of the bowling ball cannot exceed the initial momentum of the golf ball because that would imply the system has gained momentum.
C. The first friend:
By the Law of Conservation of Momentum , . Since the initial momentum of the golf ball was in one direction, after the collision, it went in another direction, thus gaining negative momentum with respect to the bowling ball's momentum. To offset this negative momentum, the bowling ball's momentum must be greater than the initial momentum of the golf ball.
D. The second friend:
Not only would the collision violate the Law of Conservation of Momentum , , but it would violate the principle of elastic collisions . The "negative" momentum of the golf ball is impossible, for then it would not be transfer its initial momentum to the bowling ball (think billiard balls: when one ball strikes another, its momentum is transferred to the ball receiving the hit; but the striking billiard ball never changes its direction of motion).

Details and Assumptions
-
For simplicity purposes, you may assume the interaction takes place in 1 dimensional space (linear motion), and 1 dimension of time (and 1 for every other cosmic parameter beyond 7D hyperverses).
-
The golf ball and the bowling ball are the only two objects in the universe before the interaction, during the interaction, and after.
Problem credit: Conceptual Physics: Special Edition Series - Paul G. Hewitt.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
A brief definition of momentum:
We all know that a heavy truck is harder to stop than a small car moving at the same speed. We state this fact by saying that the truck has more momentum than the car. By momentum we mean inertia in motion. More specifically, momentum is defined as the product of the mass of an object and its velocity; that is,
Momentum = mass × velocity 1 .
Law of Conservation of Momentum:
Net momentum before collision = Net momentum after collision
m v b e f o r e = m v a f t e r .
First of all, note that v is a vector quantity (and hence Net momentum ), and thus we can expect negative values and cancellations of sorts. Second, note that the masses of the two objects are different (commonsense assumption). Third of all, note that our SYSTEM consists of the bowling ball, and the golf ball. Now we're ready. Let's dive in:
Short answer:
After the collision, the bowling ball moves to the right, and the golf ball moves to the left. Because the total momentum of the system must be to the right, any motion of the golf ball to the left means that the momentum of the bowling ball must be that much bigger to the right. So, if the golf ball moves to the left at all, then the bowling ball has more momentum than the golf ball had initially. But the total momentum of the system is conserved.
The answer is C .
Thorough analysis:
Reasons to read "Thorough Analysis:"
Encompasses the concepts of
Impulse, Momentum, Newton's Laws of Motion, Bouncing, Elasticity, Systems
Let's break the event into three parts: 1. Before collision. 2. During collision. 3. After collision.
Let's say the golf ball begins moving to the right toward the bowling ball at rest. This implies that the golf ball has a momentum, and the bowling ball has none. So, the condition of the system before collision can be expressed as follows:
Assume motion to the right as positive. Then,
m v g o l f b a l l + m v b o w l i n g b a l l
= m v g o l f b a l l + m ( 0 ) b o w l i n g b a l l
= m v g o l f b a l l
Now, during the collision, it gets a bit more complicated. A few factors are involved: elastic collisions, impulse, and, of course, conservation of momentum. Let me digress to bouncing for a bit:
If a flowerpot falls from a shelf onto your head, you may be in trouble. If it bounces from your head, you may be in more serious trouble. Why? Well, this digresses from the problem at hand; we just want to stick with conservation of momentum here to avoid confusion. Read more about it below the solution.
Basically, if you try in real life, throwing a golf ball at a bowling ball will cause it to bounce back, and thus gain "negative" momentum. Does this violate the Law? Not at all:
Due to the fact that the momentum of the ENTIRE SYSTEM is rightward before the collision, the momentum after the collision has to remain the same - rightward. Now, since the golf ball does bounce upon impact, and does gain negative momentum with respect to the bowling ball, then in order to maintain a rightward momentum, this means that the momentum of the bowling ball MUST BE GREATER than the initial momentum of the golf ball:
m v b e f o r e c o l l i s i o n = m v a f t e r c o l l i s i o n
To avoid confusion, let the momentum of the golf ball be p and the momentum of the bowling ball be P .
p b e f o r e + 0 P b e f o r e = p a f t e r + P a f t e r
p b e f o r e = p a f t e r + P a f t e r
Solving,
P a f t e r = p b e f o r e − p a f t e r
Since the momentum of the golf ball after the collision ( p a f t e r ) is negative, subtracting it will add to p b e f o r e (initial momentum of the golf ball). And thus,
P a f t e r > p b e f o r e
Momentum of bowling ball after collision > Initial momentum of golf ball
Oh, and for those who are asking "But the bowling ball barely even moves, so isn't its momentum close to zero?" This is due to radically different masses of the balls. Have a visual:
BOUNCING, IMPULSE, ELASTICITY
A brief definition of IMPULSE :
If you apply a brief force to a stalled automobile, you produce a change in its momentum. Apply the same force over an extended period of time, and you produce a greater change in the automobile's momentum:
Impulse = Force × time → Impulse = F t
The greater the impulse exerted on something, the greater will be the change in momentum:
Impulse = change in momentum → F t = Δ ( m v ) . 2
If a flowerpot falls from a shelf onto your head, you may be in trouble. If it bounces from your head, you may be in more serious trouble. Why? Let's dive in:
Because impulses are greater when an object bounces. The impulse required to bring an object to stop and then to "throw it back again" is greater than the impulse required merely to bring the object to a stop.
Suppose, for example, that you catch the falling pot with your hands. You provide an impulse to reduce its momentum to zero. If you throw the pot upward again, you have to provide additional impulse. This increased amount of impulse is the same that your head supplies if the flowerpot bounces from it 3 .
So now you may be asking, what provides this impulse?
The bowling ball doesn't have hands to toss the golf ball back again. But neither does your head. What's involved is another concept called elasticity . Elasticity is the property of a material to change shape when a deforming force acts upon it and return to its original shape when the force is removed. If an object is elastic, the internal physical composition of the object is structured in a way that allows the object to compress and stretch easily (such as springs, mattresses, and rubber bands). With the golf ball, the elasticity is less apparent, but it's there (the full reason for bouncing cannot be discussed without involving kinetic and potential energy along with other parameters, but this digresses from mechanics so we'll refrain from it).
So, when the golf ball collides with the bowling ball, the golf ball impresses an external force on the bowling ball, causing it to accelerate (Newton's First Law+Newton's Second Law). Meanwhile, the bowling ball impresses an equal and opposite (Newton's Third Law) impulse (since the interaction time is the same), serving as not only a stopping force, but as a deforming force, causing the golf ball to compress and stretch, thus bouncing it off. Upon stretching, the golf ball impresses an equal and opposite force (a push-off force) on the bowling ball, and gains velocity in the negative direction. The amount of momentum provided by the bowling ball's impulse is equal and opposite to the impulse provided by the golf ball ( F t ⇒ − F t ); and thus, in addition to the initial transfer of momentum from the golf ball to the bowling ball, we have a transfer of momentum due to impulse. Hence, the momentum of the bowling ball after the collision is greater than the initial momentum of the golf ball:
Net momentum before event = Net momentum after event
Laws obeyed:
Newton's First Law
Newton's Second Law
Newton's Third Law
Law of Conservation of Momentum;
Laws violated:
None.
P.S. Answer D cannot apply to this case because it is an interaction between two objects of nearly identical size, mass, and elastic properties, whereas a bowling ball and a golf ball are radically different in all those three respects. And answer B is simply a trickster. In fact, the entire problem is. So don't be hard on yourself if you got this wrong; it took me an hour to fully come up with the right answer.
Isn't it beautiful to see so many concepts of physics involved in one little collision? And we haven't even discussed any quantum interactions involved!
Physics is indeed the supreme Law of the Universe.
1,2,3 - the paragraphs (2 - the entire definition) are copied directly from the book. The rest are principles applied from, but not taken directly out of, the book.