Concurrence
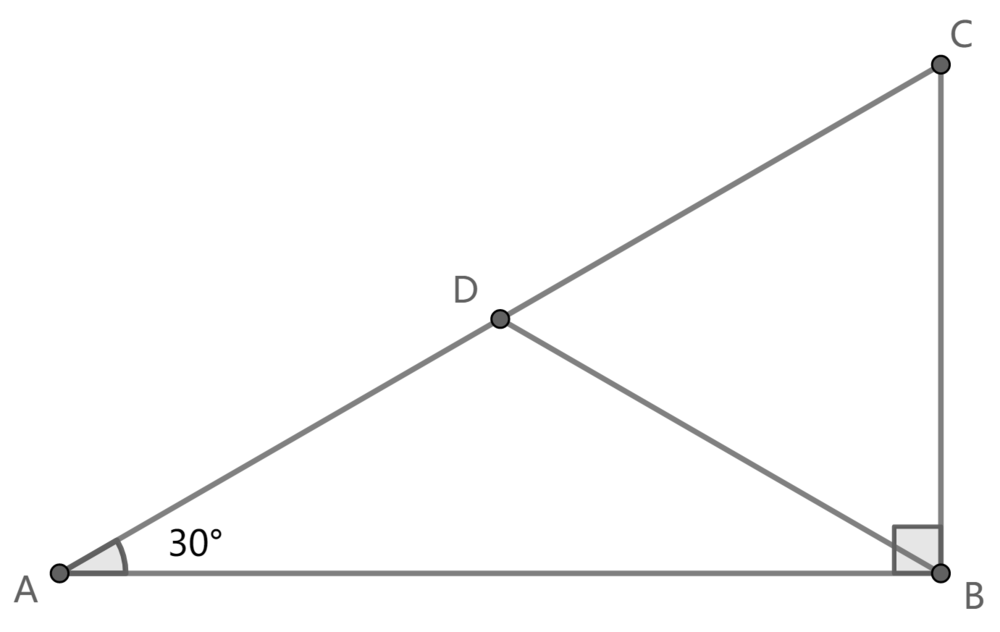 In right triangle
A
B
C
,
∠
A
B
C
=
9
0
∘
,
∠
B
A
C
=
3
0
∘
and
D
is the midpoint of side
A
C
.
In right triangle
A
B
C
,
∠
A
B
C
=
9
0
∘
,
∠
B
A
C
=
3
0
∘
and
D
is the midpoint of side
A
C
.
Does the intersection point of perpendicular bisectors of A C and B D lie on A B ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
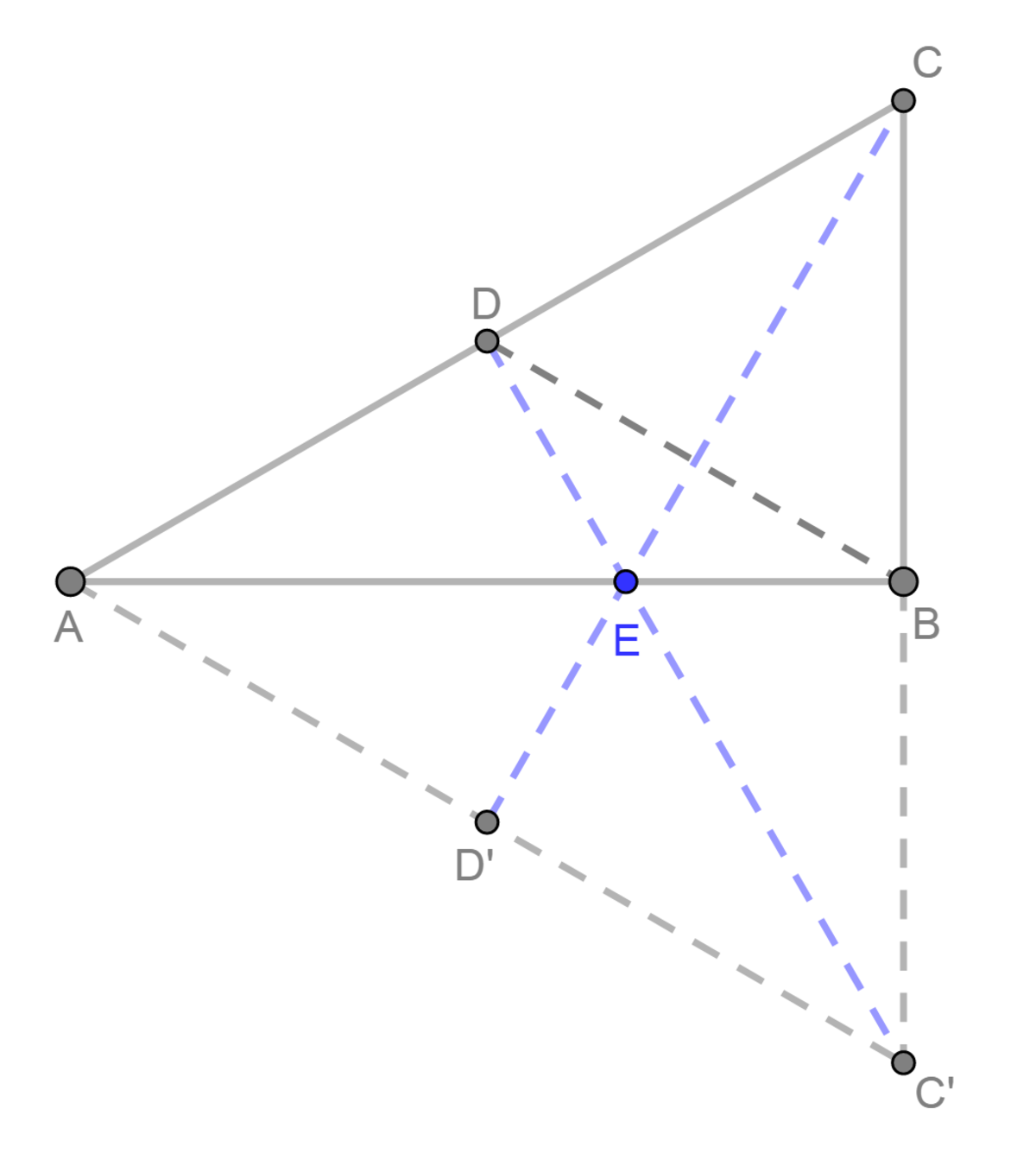 Add a point
C
′
symmetric to
C
about
A
B
to get an equilateral triangle
△
A
C
C
′
.
B
D
is parallel to
A
C
′
, as it connects the midpoints of
A
C
and
C
C
′
, and because
△
A
C
C
′
is equilateral,
B
D
and
A
C
′
share a common perpendicular bisector -
C
D
′
.
C
′
D
is a perpendicular bisector of
A
C
, so
A
B
,
C
′
D
and
C
D
′
all intersect at
E
- the centroid/incenter/circumcenter/orthocenter of
△
A
C
C
′
.
Add a point
C
′
symmetric to
C
about
A
B
to get an equilateral triangle
△
A
C
C
′
.
B
D
is parallel to
A
C
′
, as it connects the midpoints of
A
C
and
C
C
′
, and because
△
A
C
C
′
is equilateral,
B
D
and
A
C
′
share a common perpendicular bisector -
C
D
′
.
C
′
D
is a perpendicular bisector of
A
C
, so
A
B
,
C
′
D
and
C
D
′
all intersect at
E
- the centroid/incenter/circumcenter/orthocenter of
△
A
C
C
′
.
Drop a perpendicular to A C from D . Say it intersects A B at E . Since B C D is equilateral, the perpendicular from C bisects B D , so all that is required is to show that that perpendicular goes through E , i.e. to show that C E is perpendicular to B D .
To see this, consider right triangles C D E and C B E . These share a hypotenuse, C E , and have congruent legs C D and C B . So they are congruent. Hence ∠ D C E = ∠ B C E = 2 1 ∠ A C B = 3 0 ∘ . The fact that C E bisects ∠ B C D shows that C E is perpendicular to B D : e.g. if C E and B D intersect at F , it's clear that ∠ C F B = 1 8 0 ∘ − 3 0 ∘ − 6 0 ∘ = 9 0 ∘ .
Choose a coordinate system with A at (0,0). Then, by properties of 30-60-90 triangles, the coordinates of the other points are D(Sqrt(3)/2, 1/2), C(Sqrt(3), 1), B(Sqrt(3), 0). If L1 is the perpendicular bisector of AC, we find L1 has slope of -Sqrt(3). Since it passes through D, it's equation is L1(x) = 1/2 - Sqrt(3)*(x-Sqrt(3) / 2). This intersects AB when it's y-coordinate is 0. Doing the algebra yields x = 2/Sqrt(3). Similarly, we can find an equation for L2, the perpendicular bisector of DB. Setting that equation equal to zero also yields x = 2/Sqrt(3), which is the same coordinate as the zero of L1. Therefore, they do meet on AB (at a distance of 2/Sqrt(3) units from A.