Conditioned For Maximum Time!
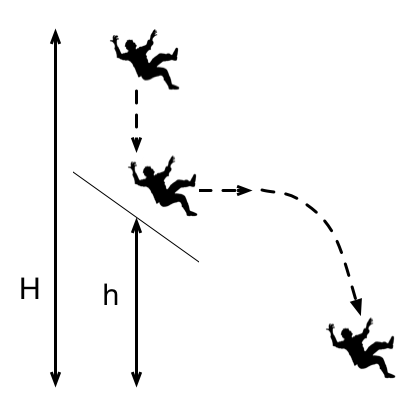
A body falling freely from a given height H hits an inclined plane at a height h , in a perfectly elastic collision. As a result of this impact, the direction of the body becomes horizontal. For what value of H h the body will take maximum time to reach the ground?
The answer is 0.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The collision will convert all the vertical velocity to horizontal velocity. Since we are dealing with time we can consider that after the collision the vertical velocity again became 0
For Time before collision
(H-h) = 0T + 2 1 g T 2
Therefore T = g 2 ( H − h )
After collision,
h = 0t + 2 1 g t 2
=> t = g 2 ( h )
Therefore total time = g 2 H ( 1 − H h + H h )
Now time will be maximum when H h = 2 1 = 0 . 5
The body initially falls H − h from a zero vertical velocity, which takes a time of g 2 ( H − h ) . Then immediately after the collision, it once again has a zero vertical component of velocity, so it takes a time of g 2 h to fall the remaining h .
The total time is g 2 ( H − h ) + g 2 h = g 2 H ( 1 − H h + H h ) which, for a given H , is maximized when 1 − H h + H h is maximized, at H h = 2 1