This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
But what if a,b,c are 0.
Log in to reply
Good point. If a , b , c are all equal to 0 then the expression is indeterminate, so I took it as implicit that this wasn't the case. The asker should probably make this explicit in the question.
Note that if not all three are 0 then at least two must be non-zero, in which case at least one of b or c is non-zero. As long as one of them is non-zero then we are guaranteed that b 2 + c 2 + b c > 0 , in which case the expression will be determinate.
Isn't it given clearly that abc is not eaual to zero, i.e. neither of them is zero.
Wow, the trick here is to see that since
a+b+c=0,
a+b=-c and b+c=-a and a+c=-b
This is an important step and afterwards the solution is obvious.
I plugged values in for a,b,&c. Let a = .5 Let b = .3 Let c = -.8
Because a+b+c =0
When I plug those values in for the first fraction, the result is .49/.49 which is equal to 1.
When I plug those values in for the second fraction, the result is .49/.49 which is equal to 1.
1+1=2
There's your answer!
let 1=1 b=2 c=-3
Log in to reply
But the challenge is to solve it using variable
If you plug in c = − a − b , it's not hard to see that both fractions are equal to 1 no matter which values you choose.
Ha Ha Ha ...... I did the same ^_^
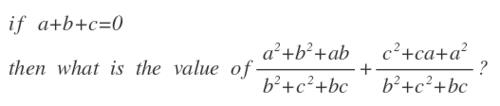
We already have a common denominator, so we'll focus on the sum of the numerators. Since a + b + c = 0 , the sum of the numerators can be rewritten as
( a + b ) 2 − a b + ( a + c ) 2 − a c = ( − c ) 2 + ( − b ) 2 − a ∗ ( b + c ) = b 2 + c 2 + ( b + c ) 2 = 2 ∗ ( b 2 + c 2 + b c ) .
Dividing this by the common denominator gives us an answer of 2 .